Борис Тарасов - Паскаль

Применяя метод неделимых к различным величинам, преобразуя одни виды суммирования в другие, Паскаль в геометрической форме получил фундаментальные результаты, относящиеся к так называемым криволинейным в двойным интегралам, с помощью наглядных конкретных примеров и ясных доказательств, искусного использования приемов современной ему и античной математики упорядочил многие интеграционные проблемы, освободив их от нечетких и приблизительных решений. До прямого открытия интегрального исчисления Паскалю оставалось сделать лишь шаг — определить формальные операции интегрирования и дать его особый вычислительный алгоритм. Но Паскаль этого шага не сделал. Как и прежде, помешали его «геометризм» и антиалгебраическая настроенность, использование прямых конкретных методов. Поэтому славу первооткрывателей интегрального и дифференциального исчисления делят между собой Ньютон и Лейбниц, хотя некоторые исследователи и причисляют Паскаля к ним, исходя из возможности легкого перевода исключительно геометрических рассуждений Блеза на абстрактный язык анализа бесконечно малых.

О возможности такого перевода и извлечения алгоритма из математических трудов Паскаля свидетельствует и признание Лейбница, которое относится к «Трактату о синусах четверти круга» Блеза, связанному с исследованием циклоиды. В 1673 году по совету Гюйгенса немецкий философ познакомился с этим трактатом и, как он сам замечает, был внезапно озарен новым светом. Особое внимание Лейбница привлек чертеж с бесконечно малым треугольником, используемым Блезом для преобразования интегральных сумм. Лейбниц назвал этот треугольник характеристическим, увидев в нем один из основных элементов дифференциального исчисления, и с его помощью подошел к формулировке самих принципов этого исчисления.

Пусть нам дана, пишет Паскаль в лемме «Трактата...», четверть круга ABC (см. рис. 5), где радиус AB рассмат-

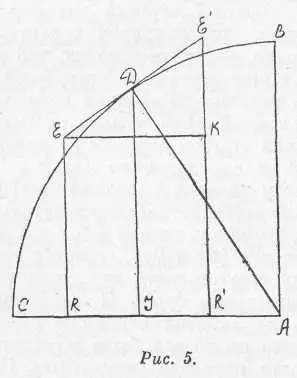
ривается как ось, а радиус АС — как основание. Возьмем на дуге окружности произвольную точку Д, из которой на основание проводится линия синуса ДI и радиус АД и через которую проходит также касательная ЕЕ'. Из точек E и E' на основание АС опускаются перпендикуляры ER и E'R'. Затем Паскаль строит треугольник ЕКЕ' (данный треугольник Лейбниц и назвал характеристическим), который подобен треугольнику ДIА. Это подобие дает ему пропорцию:

AD/DI= EE1/ЕК,

в которой отношение бесконечно малых величин (EE1/EK) выражено отношением конечных величин AD/DI, и равенство:

ДIxЕЕ' = АДxЕК, илиДIxЕЕ' = АДxRR'.

Если же разделить какую-либо дугу четверти круга на малые части и заменить отрезки касательных эквивалентными им при переходе к пределу малыми дугами, то при интегрировании обеих частей этого равенства получается теорема, которая в «Трактате...» Паскаля звучит так: «Сумма синусов какой-либо дуги четверти круга равна отрезку основания между крайними синусами, умноженному на радиус».

«Лейбниц, — пишет советский историк математики И. Б. Погребысский, рассматривая характеристический треугольник Паскаля, — сразу заметил, что это построение и связанный с ним переход от отношения бесконечно малых величин к отношению величин конечных справедливы для любой кривой. Надо только рассматривать АД не как радиус, а как отрезок нормали к кривой, проведенный до пересечения с основанием (осью абсцисс). Это было важным шагом на пути к созданию дифференциального исчисления: характеристический треугольник при переходе к пределу, когда его катеты (^ х и ^ у) становятся бесконечно малыми (dx и dy), остается все время подобным конечному треугольнику, что позволяет уверенно действовать с отношением dy/dx. И Лейбница удивляло, как это Паскаль не заметил общности своего построения, «словно у него на глазах была повязка».

О естественности перевода результатов Паскаля при решении задач в связи с циклоидой на терминологию специальных понятий и абстрактной символики интегрального исчисления, а также о четкости его мышления и ясности языка можно судить и по высказыванию известных французских математиков, выступивших под псевдонимом Н. Бурбаки: «Валлис в 1655 году и Паскаль в 1658 году составили каждый для своего употребления языки алгебраического характера, в которых, не записывая ни единой формулы, они дают формулировки, которые можно немедленно, как только будет понят их механизм, записать в формулах интегрального исчисления. Язык Паскаля особенно ясен и точен; и если не всегда понятно, почему он отказался от применения алгебраических обозначений не только Декарта, но и Виета, все же нельзя не восхищаться его мастерством, которое могло проявиться лишь на основе совершенного владения языком».