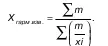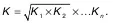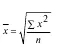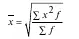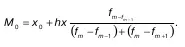Средняя гармоническая взвешенная, тождественна средней арифметической: Когда произведения fxодинаковы или равны
единицы (m= 1) применяется средняя гармоническая
простая:
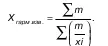
где х–отдельные варианты; n– число.
Если имеется n коэффициентов роста, то формула среднего коэффициента:
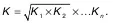
Средняя геометрическая равна корню степени nиз произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего.
Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число.
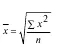
Средняя квадатическая взвешенная равна:
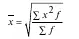
31. Структурные средние величины. Мода и медиана
Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними.К ним относятся мода и медиана.
Мода (Мо)– чаще всего встречающийся вариант.
Модойназывается значение признака, которое соответствует максимальной точке теоретической кривой распределений.
Мода представляет наиболее часто встречающееся или типичное значение. Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен.
В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность). В пределах интервала надо найти то значение признака, которое является модой.
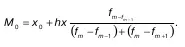
где x 0– нижняя граница модального интервала;
h– величина модального интервала;
f m– частота модального интервала;
f m - 1 – частота интервала, предшествующего модальному;
f m + 1 – частота интервала, следующего за модальным.
Мода зависит от величины групп, от точного положения границ групп.
31б Мода– число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя).
Медиана (M e)– это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.
Медиана– это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.
Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.
Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал:
Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.
Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака.Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.
Колебания отдельных значений характеризуют показатели вариации.
Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариациейпонимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.
Читать дальше
Конец ознакомительного отрывка
Купить книгу