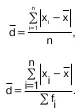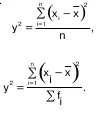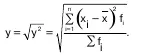Лидия Щербина - Общая теория статистики

Медиана и мода в отличие от средней арифмети–ческой не погашают индивидуальных различий в зна–чениях варьирующего признака и поэтому являются дополнительными и очень важными характеристика–ми статистической совокупности. На практике они ча–сто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содер–жит некоторое количество единиц с очень большим или очень малым значением варьирующего признака.

Вариационными называют ряды распределени построенные по количественному признаку. Значени количественных признаков у отдельных единиц сов купности непостоянны, более или менее различают между собой. Такое различие в величине признака н сит название вариации. Отдельные числовые значени признака, встречающиеся в изучаемой совокупност называют вариантами значений. Наличие вариаци у отдельных единиц совокупности обусловлено влияние большого числа факторов на формирование уровня при: нака.

Расположения всех вариантов значений признай в возрастающем или убывающем порядке. Процесс назь вают ранжированием ряда. Ранжированный ряд сра дает общее представление о значениях, которые прин мает признак в совокупности.

Для измерения вариации признака применяют различные абсолютные и относительные показател К абсолютным показателям вариации относятся средне линейное отклонение, размах вариации, дисперсия, сре нее квадратическое отклонение.

Среднее линейное отклонение представляет с бой среднюю арифметическую из абсолютных значени отклонений отдельных вариантов от их средней ариф метической:

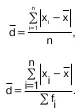
Дисперсия ( σ 2) – средняя из квадратов отклонений вариантов значений признака от их средней величины:

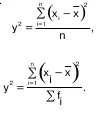
Среднее квадратическое отклонение ( σ ) пред–ставляет собой корень квадратный из дисперсии:

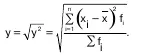
Относительные показатели колеблемости:

Коэффициент вариации – наиболее часто при–меняемый показатель относительной колеблемости, ха–рактеризующий однородность совокупности. Совокуп–ность считается однородной, если коэффициент вариации не превышает 33% для распределений, близ–ких к нормальному.

Статистическое наблюдение можно организо–вать как сплошное и несплошное. Сплошное предус–матривает обследование всех единиц изучаемой со–вокупности явления, несплошное – лишь ее части. К несплошному относится и выборочное наблюде–ние.

Целью выборочного наблюдения является полу–чение информации прежде всего для определения сводных обобщающих характеристик всей изучаемой совокупности. Соблюдение принципа позволяет по–лучить такую совокупность единиц, которая по инте–ресующим исследователя признакам представляет всю изучаемую совокупность, т. е. является репрезен–тативной (представительной).

При проведении выборочного наблюдения об–следуются не все единицы изучаемого объекта, а лишь ее некоторая часть, специальным образом отобранная. Первый принцип отбора – обеспечение случайности – заключается в том, что при отборе каждой из единиц изучаемой совокупности обеспечи–вается равная возможность попасть в выборку. Слу–чайный отбор можно обеспечить только при соблюде–нии определенной методики.

Второй принцип отбора – обеспечение доста–точного числа отобранных единиц – тесно связан с понятием репрезентативности выборки. Понятие репрезентативности отобранной совокупности еди–ниц не следует понимать как ее представительность во всех отношениях. Такое представительство обес–печить практически невозможно. Любое выборочное наблюдение проводится с определенной целью и четко сформулированными конкретными зада–чами, понятие репрезентативности должно быть связано с целью и задачами исследования. Отобран–ная из всей изучаемой совокупности часть должна быть репрезентативной прежде всего в отношении тех признаков, которые изучаются или оказывают су–щественное влияние на формирование сводных обоб–щающих характеристик.