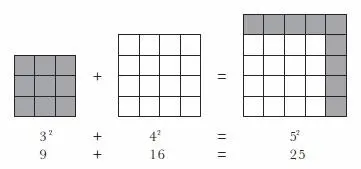Simon Singh - Fermat’s Last Theorem

There are two approaches to the problem:

(1) The scientific approach

The scientist would try to solve the problem by experimenting, and after trying out a few dozen arrangements would discover that they all fail. Eventually the scientist believes that there is enough evidence to say that the board cannot be covered. However, the scientist can never be sure that this is truly the case because there might be some arrangement which has not been tried which might do the trick. There are millions of different arrangements and it is only possible to explore a small fraction of them. The conclusion that the task is impossible is a theory based on experiment, but the scientist will have to live with the prospect that one day the theory may be overturned.

(2) The mathematical approach

The mathematician tries to answer the question by developing a logical argument which will derive a conclusion which is undoubtedly correct and which will remain unchallenged forever. One such argument is the following:

• The corners which were removed from the chessboard were both white. Therefore there are now 32 black squares and only 30 white squares.

• Each domino covers two neighbouring squares, and neighbouring squares are always different in colour, i.e. one black and one white.

• Therefore, no matter how they are arranged, the first 30 dominoes laid on the board must cover 30 white squares and 30 black squares.

• Consequently, this will always leave you with one domino and two black squares remaining.

• But remember all dominoes cover two neighbouring squares, and neighbouring squares are opposite in colour. However, the two squares remaining are the same colour and so they cannot both be covered by the one remaining domino. Therefore, covering the board is impossible!

This proof shows that every possible arrangement of dominoes will fail to cover the mutilated chessboard. Similarly Pythagoras constructed a proof which shows that every possible right-angled triangle will obey his theorem. For Pythagoras the concept of mathematical proof was sacred, and it was proof that enabled the Brotherhood to discover so much. Most modern proofs are incredibly complicated and following the logic would be impossible for the layperson, but fortunately in the case of Pythagoras’ theorem the argument is relatively straightforward and relies on only senior school mathematics. The proof is outlined in Appendix 1.

Pythagoras’ proof is irrefutable. It shows that his theorem holds true for every right-angled triangle in the universe. The discovery was so momentous that one hundred oxen were sacrificed as an act of gratitude to the gods. The discovery was a milestone in mathematics and one of the most important breakthroughs in the history of civilisation. Its significance was twofold. First, it developed the idea of proof. A proven mathematical result has a deeper truth than any other truth because it is the result of step-by-step logic. Although the philosopher Thales had already invented some primitive geometrical proofs, Pythagoras took the idea much further and was able to prove far more ingenious mathematical statements. The second consequence of Pythagoras’ theorem is that it ties the abstract mathematical method to something tangible. Pythagoras showed that the truth of mathematics could be applied to the scientific world and provide it with a logical foundation. Mathematics gives science a rigorous beginning and upon this infallible foundation scientists add inaccurate measurements and imperfect observations.

The Pythagorean Brotherhood invigorated mathematics with its zealous search for truth via proof. News of their success spread and yet the details of their discoveries remained a closely guarded secret. Many requested admission to the inner sanctum of knowledge, but only the most brilliant minds were accepted. One of those who was blackballed was a candidate by the name of Cylon. Cylon took exception to his humiliating rejection and twenty years later he took his revenge.

During the sixty-seventh Olympiad (510 BC) there was a revolt in the nearby city of Sybaris. Telys, the victorious leader of the revolt, began a barbaric campaign of persecution against the supporters of the former government, which drove many of them to seek sanctuary in Croton. Telys demanded that the traitors be returned to Sybaris to suffer their due punishment, but Milo and Pythagoras persuaded the citizens of Croton to stand up to the tyrant and protect the refugees. Telys was furious and immediately gathered an army of 300,000 men and marched on Croton, where Milo defended the city with 100,000 armed citizens. After seventy days of war Milo’s supreme generalship led him to victory and as an act of retribution he turned the course of the river Crathis upon Sybaris to flood and destroy the city.

Despite the end of the war, the city of Croton was still in turmoil because of arguments over what should be done with the spoils of war. Fearful that the lands would be given to the Pythagorean elite, the ordinary folk of Croton began to grumble. There had already been growing resentment among the masses because the secretive Brotherhood continued to withhold their discoveries, but nothing came of it until Cylon emerged as the voice of the people. Cylon preyed on the fear, paranoia and envy of the mob and led them on a mission to destroy the most brilliant school of mathematics the world had ever seen. Milo’s house and the adjoining school were surrounded, all the doors were locked and barred to prevent escape and then the burning began. Milo fought his way out of the inferno and fled, but Pythagoras, along with many of his disciples, was killed.

Mathematics had lost its first great hero, but the Pythagorean spirit lived on. The numbers and their truths were immortal. Pythagoras had demonstrated that more than any other discipline mathematics is a subject which is not subjective. His disciples did not need their master to decide on the validity of a particular theory. A theory’s truth was independent of opinion. Instead the construction of mathematical logic had become the arbiter of truth. This was the Pythagoreans’ greatest contribution to civilisation – a way of achieving truth which is beyond the fallibility of human judgement.

Following the death of their founder and the attack by Cylon, the Brotherhood left Croton for other cities in Magna Graecia, but the persecution continued and eventually many of them had to settle in foreign lands. This enforced migration encouraged the Pythagoreans to spread their mathematical gospel throughout the ancient world. Pythagoras’ disciples set up new schools and taught their students the method of logical proof. In addition to their proof of Pythagoras’ theorem, they also explained to the world the secret of finding so-called Pythagorean triples.

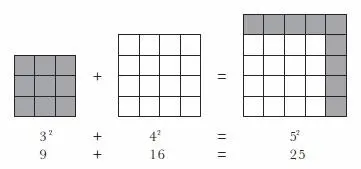
Figure 3. Finding whole number solutions to Pythagoras’ equation can be thought of in terms of finding two squares which can be added together to form a third square. For example, a square made of 9 tiles can be added to a square of 16 tiles, and rearranged to form a third square made of 25 tiles.

Pythagorean triples are combinations of three whole numbers which perfectly fit Pythagoras’ equation: x 2+ y 2= z 2For example, Pythagoras’ equation holds true if x = 3, y = 4 and z = 5:

Another way to think of Pythagorean triples is in terms of rearranging squares. If one has a 3 × 3 square made of 9 tiles, and a 4 × 4 square made of 16 tiles, then all the tiles can be rearranged to form a 5 × 5 square made of 25 tiles, as shown in Figure 3.