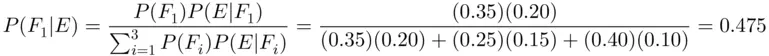
We note that the posterior probability of 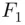 , given E , is 0.475, while the prior probability of
, given E , is 0.475, while the prior probability of 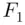 was
was 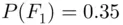 . We sometimes say that the prior information about
. We sometimes say that the prior information about  has been updated in light of the information that E occurred to the posterior probability of
has been updated in light of the information that E occurred to the posterior probability of 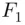 , given E , through Bayes's theorem.
, given E , through Bayes's theorem.
PRACTICE PROBLEMS FOR SECTIONS 3.5 AND 3.6
1 A regular die is rolled. If the number that showed up is odd, what is the probability that it is 3 or 5?
2 Three balanced coins are tossed simultaneously. What is the probability that exactly two heads appear given that at least one head has appeared?
3 Suppose that and are five mutually exclusive and exhaustive events in a sample space S, and suppose that , and . Another event E in S is such that , and . Find the probabilities , and .
4 Suppose that four attorneys , and deal with all the criminal cases in a district court. The following table gives the percentages of the cases that each of these attorneys handles, and also the probability that each loses the case;AttorneyProbability of handling the caseProbability of losing the case0.400.150.250.300.250.200.100.40Suppose that a criminal case was lost in the court. Find the probability that this case was handled by Attorney .
5 Suppose that a random experiment consists of randomly selecting one of four coins , and , tossing it and observing whether a head or a tail occurs. Further suppose that the coins , and are biased such that the probabilities of a head occurring for coins , and are 0.9, 0.75, and 0.60, respectively, while the fourth coin is a fair coin.If the outcome of the experiment was a head, find the probability that coin was tossed.If the outcome of the experiment was a tail, find the probability that coin was tossed.
6 An industry uses three methods, and to manufacture a part. Of all the parts manufactured, 45% are produced by method , 32% by method , and the rest 23% by method . Further it has been noted that 3% of the parts manufactured by method are defective, while 2% manufactured by method and 1.5% by method are defective. A randomly selected part is found to be defective. Find the probability that the part was manufactured by (a) method , (b) method .
7 There are four roads connecting location A and location B. The probabilities that if a person takes Road I, Road II, Road III, or Road IV from location A to B, then he/she will arrive late because of getting stuck in the traffic are 0.3, 0.20, 0.60, and 0.35, respectively. Suppose that a person chooses a road randomly and he/she arrives late. What is the probability that the person chose to take Road III?
8 Suppose that in a ball‐bearing manufacturing plant four machines , and manufacture 36%, 25%, 23%, and 16% of the ball bearings, respectively. It is observed that the four machines produce 2%, 2.5%, 2.6%, and 3% defective ball bearings, respectively. If the ball bearings manufactured by these machines are mixed in a well‐mixed lot and then a randomly selected ball bearing is found to be defective, find the probability that the defective ball bearing is manufactured by (a) machine , (b) machine , (c) machine , (d) machine .
9 An urn contains five coins of which three are fair, one is two‐headed and one is two‐tailed. A coin is drawn at random and tossed twice. If a head appears both times, what is the probability that the coin is two‐headed?
3.7 Introducing Random Variables
Suppose that a finite sample space S consists of m elements 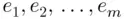 . There are
. There are 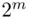 possible events that can be formed from these elements, provided that the empty event
possible events that can be formed from these elements, provided that the empty event 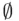 and the entire sample space S are counted as two of the events. This is revealed by the fact that we have the choice of selecting or not selecting each of the m elements in making up an event. Rarely, if ever, is one interested in all these
and the entire sample space S are counted as two of the events. This is revealed by the fact that we have the choice of selecting or not selecting each of the m elements in making up an event. Rarely, if ever, is one interested in all these 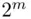 events and their probabilities. Rather, the interest lies in a relatively small number of events produced by specified values of some function defined over the elements of a sample space. For instance, in the sample space S of the
events and their probabilities. Rather, the interest lies in a relatively small number of events produced by specified values of some function defined over the elements of a sample space. For instance, in the sample space S of the 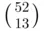 possible hands of 13 bridge cards, we are usually interested in events such as getting two aces, or eight spades, or 10 honor cards, and so on.
possible hands of 13 bridge cards, we are usually interested in events such as getting two aces, or eight spades, or 10 honor cards, and so on.
A real and single‐valued function 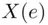 defined on each element e in the sample space S is called a random variable . Suppose that
defined on each element e in the sample space S is called a random variable . Suppose that 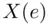 can take on the values
can take on the values 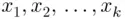 . Let
. Let 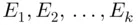 be the events that are mutually exclusive and exhaustive in the sample space S , for which
be the events that are mutually exclusive and exhaustive in the sample space S , for which 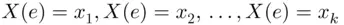 , respectively. Let
, respectively. Let  . Then, we say that
. Then, we say that 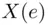 is a random variable defined over the sample space S and is a discrete random variable which takes the values
is a random variable defined over the sample space S and is a discrete random variable which takes the values 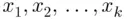 with the probabilities
with the probabilities 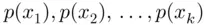 , respectively. Since
, respectively. Since 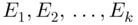 are disjoint and their union is equal to the entire sample space S , we have
are disjoint and their union is equal to the entire sample space S , we have
Читать дальше

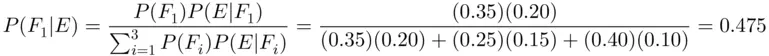
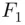 , given E , is 0.475, while the prior probability of
, given E , is 0.475, while the prior probability of 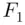 was
was 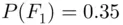 . We sometimes say that the prior information about
. We sometimes say that the prior information about  has been updated in light of the information that E occurred to the posterior probability of
has been updated in light of the information that E occurred to the posterior probability of 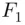 , given E , through Bayes's theorem.
, given E , through Bayes's theorem.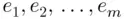 . There are
. There are 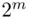 possible events that can be formed from these elements, provided that the empty event
possible events that can be formed from these elements, provided that the empty event 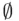 and the entire sample space S are counted as two of the events. This is revealed by the fact that we have the choice of selecting or not selecting each of the m elements in making up an event. Rarely, if ever, is one interested in all these
and the entire sample space S are counted as two of the events. This is revealed by the fact that we have the choice of selecting or not selecting each of the m elements in making up an event. Rarely, if ever, is one interested in all these 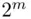 events and their probabilities. Rather, the interest lies in a relatively small number of events produced by specified values of some function defined over the elements of a sample space. For instance, in the sample space S of the
events and their probabilities. Rather, the interest lies in a relatively small number of events produced by specified values of some function defined over the elements of a sample space. For instance, in the sample space S of the 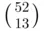 possible hands of 13 bridge cards, we are usually interested in events such as getting two aces, or eight spades, or 10 honor cards, and so on.
possible hands of 13 bridge cards, we are usually interested in events such as getting two aces, or eight spades, or 10 honor cards, and so on.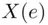 defined on each element e in the sample space S is called a random variable . Suppose that
defined on each element e in the sample space S is called a random variable . Suppose that 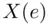 can take on the values
can take on the values 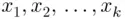 . Let
. Let 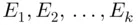 be the events that are mutually exclusive and exhaustive in the sample space S , for which
be the events that are mutually exclusive and exhaustive in the sample space S , for which 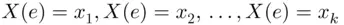 , respectively. Let
, respectively. Let  . Then, we say that
. Then, we say that 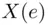 is a random variable defined over the sample space S and is a discrete random variable which takes the values
is a random variable defined over the sample space S and is a discrete random variable which takes the values 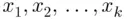 with the probabilities
with the probabilities 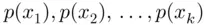 , respectively. Since
, respectively. Since 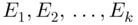 are disjoint and their union is equal to the entire sample space S , we have
are disjoint and their union is equal to the entire sample space S , we have










