An important feature of a repetitive operation is illustrated by the repetitive operation of firing a rifle at a 100‐yard target. The shooter either hits the target or misses the target. The possible outcomes “hit” or “miss” are referred to as outcomes of the experiment “firing at a target 100 yards away.” This experiment is sometimes called a random experiment . We will have more discussion of this at a later point. This important feature needs formalizing with the following definition.
Definition 3.2.1In probability theory, performing a repetitive operation that results in one of the possible outcomes is said to be performing a random experiment .
One of the basic features of repetitive operations or random experiments under specified conditions is that an outcome may vary from trial to trial. This variation leads to the analysis of the possible outcomes that would arise if a trial were performed only once. The set of all possible outcomes under specific conditions if an experiment was performed once is called the sample space of the experiment and is denoted by S . It is convenient to label an outcome in a sample space S by the letter e , and call e a sample space element or simply an element or sample point of the sample space S . The sample space S of such elements or points is generated by the operations or trials of a random experiment. Consider the following examples of elements or sample points that constitute a sample space.
Example 3.2.1(Rolling a die) If a die is rolled once, the sample space S thus generated consists of six possible outcomes; that is, the die can turn up faces numbered 1, 2, 3, 4, 5, or 6. Thus, in this case,
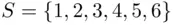
Example 3.2.2(Tossing two coins) If two coins are tossed, say a nickel and a dime, and if we designate head and tail on a nickel by H and T , respectively, and head and tail on a dime by h and t , respectively, the sample space S generated by tossing the two coins consists of four possible outcomes. We then have that
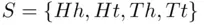
As an example, Ht denotes the outcome that the nickel, when tossed ended up showing head, while the dime, when tossed, showed tail.
Example 3.2.3(Sample space for item drawn using random sampling scheme) The sample space  for drawing five screws “at random” from a box of 100 consists of all possible sets of five screws that could be drawn from 100;
for drawing five screws “at random” from a box of 100 consists of all possible sets of five screws that could be drawn from 100;  contains 75,287,520 elements.
contains 75,287,520 elements.
Example 3.2.4(Sample space for playing cards) In dealing 13 cards from a thoroughly shuffled deck of ordinary playing cards, the sample space 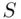 consists of the 635,013,559,600 possible hands of 13 cards that could be dealt from the 52 cards of an ordinary deck.
consists of the 635,013,559,600 possible hands of 13 cards that could be dealt from the 52 cards of an ordinary deck.
The sample spaces for these preceding examples are all finite sample spaces : they contain only a finite number of sample points. A sample space is finite as long as it contains a countable number of elements, no matter how large that number may be. For instance, in Example 3.2.4, the number of elements is very large but countable. Many problems in probability involve infinite sample spaces, that is, sample spaces containing an infinitely large number of elements that are not countable.
Example 3.2.5(Sample space for reaction times) A chemist studies the reaction time when a catalyst is added to a chemical at a certain temperature. In this experiment, the sample space 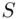 contains an indefinitely large number of elements when observing the reaction time.
contains an indefinitely large number of elements when observing the reaction time.
Example 3.2.6(Sample space for beer refills) The sample space 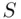 when filling a “12‐oz” can with beer with an automatic filling machine under factory conditions, would contain an indefinitely large number of elements when measuring the fluid content of the filled can.
when filling a “12‐oz” can with beer with an automatic filling machine under factory conditions, would contain an indefinitely large number of elements when measuring the fluid content of the filled can.
Suppose that S is the sample space of a random experiment that contains a finite number of outcomes or elements  . In most probability problems, we are more interested in whether or not an outcome belongs to some set E of outcomes rather than in an individual outcome. For instance, if playing the game of craps, one is usually more interested in the total number of dots that appear when the two dice are thrown than in any particular pair of dots obtained from throwing a pair of dice. The inspector who examines five screws taken “at random” from a box of 100 is not really interested in any particular one of the 75,287,250 different sets of five screws he could have drawn; he is in fact looking for the number of defective screws he gets in the five screws he draws. In other words, he is interested in whether this outcome belongs to the set of outcomes with 0 defectives, or the set with one defective, or the set with two defectives, and so on.
. In most probability problems, we are more interested in whether or not an outcome belongs to some set E of outcomes rather than in an individual outcome. For instance, if playing the game of craps, one is usually more interested in the total number of dots that appear when the two dice are thrown than in any particular pair of dots obtained from throwing a pair of dice. The inspector who examines five screws taken “at random” from a box of 100 is not really interested in any particular one of the 75,287,250 different sets of five screws he could have drawn; he is in fact looking for the number of defective screws he gets in the five screws he draws. In other words, he is interested in whether this outcome belongs to the set of outcomes with 0 defectives, or the set with one defective, or the set with two defectives, and so on.
Any set of outcomes in which there might be some particular interest is called an event . The following two examples describe two events.
Example 3.2.7(Sample space generated by tossing two coins) The event 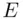 of getting exactly one head in throwing the two coins of Example 3.2.2 consists of the set of two elements
of getting exactly one head in throwing the two coins of Example 3.2.2 consists of the set of two elements 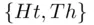 from the sample space
from the sample space 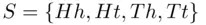 .
.
Example 3.2.8(Sample space for playing cards) Suppose that 13 cards are dealt from a deck of ordinary playing cards. Such a deck has 13 cards of each of four suits, which are spades, clubs, hearts, and diamonds. As mentioned in Example 3.2.4, there are 635,013,559,600 possible hands making up the sample space for this experiment (repetitive operation). Now suppose that we are interested in the number of possible hands (elements in 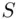 ) that contains exactly 12 spades. It turns out that this event (set) contains 507 elements, or put another way, there are 507 hands of 13 cards that contain exactly 12 spades out of the possible 635,013,559,600 hands when dealing 13 cards from a deck of 52 playing cards.
) that contains exactly 12 spades. It turns out that this event (set) contains 507 elements, or put another way, there are 507 hands of 13 cards that contain exactly 12 spades out of the possible 635,013,559,600 hands when dealing 13 cards from a deck of 52 playing cards.
Читать дальше

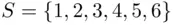
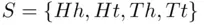
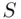 for drawing five screws “at random” from a box of 100 consists of all possible sets of five screws that could be drawn from 100;
for drawing five screws “at random” from a box of 100 consists of all possible sets of five screws that could be drawn from 100; 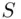 contains 75,287,520 elements.
contains 75,287,520 elements.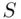 consists of the 635,013,559,600 possible hands of 13 cards that could be dealt from the 52 cards of an ordinary deck.
consists of the 635,013,559,600 possible hands of 13 cards that could be dealt from the 52 cards of an ordinary deck.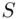 contains an indefinitely large number of elements when observing the reaction time.
contains an indefinitely large number of elements when observing the reaction time.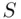 when filling a “12‐oz” can with beer with an automatic filling machine under factory conditions, would contain an indefinitely large number of elements when measuring the fluid content of the filled can.
when filling a “12‐oz” can with beer with an automatic filling machine under factory conditions, would contain an indefinitely large number of elements when measuring the fluid content of the filled can. . In most probability problems, we are more interested in whether or not an outcome belongs to some set E of outcomes rather than in an individual outcome. For instance, if playing the game of craps, one is usually more interested in the total number of dots that appear when the two dice are thrown than in any particular pair of dots obtained from throwing a pair of dice. The inspector who examines five screws taken “at random” from a box of 100 is not really interested in any particular one of the 75,287,250 different sets of five screws he could have drawn; he is in fact looking for the number of defective screws he gets in the five screws he draws. In other words, he is interested in whether this outcome belongs to the set of outcomes with 0 defectives, or the set with one defective, or the set with two defectives, and so on.
. In most probability problems, we are more interested in whether or not an outcome belongs to some set E of outcomes rather than in an individual outcome. For instance, if playing the game of craps, one is usually more interested in the total number of dots that appear when the two dice are thrown than in any particular pair of dots obtained from throwing a pair of dice. The inspector who examines five screws taken “at random” from a box of 100 is not really interested in any particular one of the 75,287,250 different sets of five screws he could have drawn; he is in fact looking for the number of defective screws he gets in the five screws he draws. In other words, he is interested in whether this outcome belongs to the set of outcomes with 0 defectives, or the set with one defective, or the set with two defectives, and so on.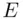 of getting exactly one head in throwing the two coins of Example 3.2.2 consists of the set of two elements
of getting exactly one head in throwing the two coins of Example 3.2.2 consists of the set of two elements 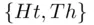 from the sample space
from the sample space 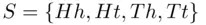 .
.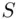 ) that contains exactly 12 spades. It turns out that this event (set) contains 507 elements, or put another way, there are 507 hands of 13 cards that contain exactly 12 spades out of the possible 635,013,559,600 hands when dealing 13 cards from a deck of 52 playing cards.
) that contains exactly 12 spades. It turns out that this event (set) contains 507 elements, or put another way, there are 507 hands of 13 cards that contain exactly 12 spades out of the possible 635,013,559,600 hands when dealing 13 cards from a deck of 52 playing cards.










