Vasily B. Novozhilov - Theory of Solid-Propellant Nonsteady Combustion

The fifth chapter considers nonsteady propellant burning in the tangential stream of combustion products. Within the framework of the phenomenological theory, the propellant burning rate response to periodically varying pressure and tangential mass flux of combustion products is investigated. An elementary acoustic perturbation in the form of a monochromatic travelling sound wave is considered. Analytical and numerical results are obtained for the simplest propellant model described by a minimal number of parameters. The role of steady‐state and nonsteady erosion contributions at small and large values of the erosion ratio is also revealed.

The following chapter deals with nonsteady combustion under external radiation. In this case, the heat transfer equation includes an additional source term, while both steady‐state and nonsteady burning laws also change. The stability of the steady‐state combustion regime is investigated in the linear approximation. The response functions of the burning rate to harmonically oscillating pressure in the presence of constant radiative flux, as well as to harmonically oscillating radiative flux, are obtained. In the linear approximation of the ZN theory, an analytical relationship between the response function to oscillating pressure, obtained at a certain initial temperature, and response function to oscillating radiative flux, obtained at the same pressure but different (lower) initial temperature, is established. The difference of initial temperatures satisfies the requirement that steady‐state burning rates with and without radiative flux are equal, and is directly proportional to radiative flux. It is likely that this relationship will be useful for obtaining experimental data on the response function to oscillating pressure.

Chapter 7presents theoretical considerations and experimental data related to combustion regimes where pressure varies according to the law, which is different from harmonic oscillations. Such processes include, for example, propellant combustion during transition from one operational regime to another (at higher or lower pressure), extinction on rapid and deep depressurization, and others.

The eighth chapter describes nonsteady propellant combustion regimes in the combustion chamber of a rocket engine. There are three time scales that are relevant for this problem: the thermal relaxation time of the heated layer of the condensed phase t c, the acoustic time t a, and the time of combustion products efflux from the chamber t ch.

If the relaxation time of the condensed phase is close to the efflux time, t c∼ t ch(which occurs in small engines at low pressures), then such regimes may be called nonacoustic. Time scales in such problems are much larger than the acoustic time. This area of research may also be referred to as propellant combustion in semi‐enclosed volume.

On the other hand, over the last few decades a specific and dedicated area of research which may be termed ‘acoustics and combustion’ has taken shape. It deals with the case where acoustic time is close to the condensed phase thermal relaxation time t a∼ t c, which leads to a possibility of sonic (in the general case nonlinear) oscillations development in the engine. The latter relation between the time scales applies to engines of large size with high pressure values in combustion chambers. The theory of such processes is still at a rudimentary stage. As an example, possible combustion regimes in a solid rocket engine with end burner grain geometry are investigated. A set of equations which allows the interaction between combustion and acoustic processes in a combustion chamber to be modelled is presented. The specific feature of the problem is the existence of the two distinctive time scales, namely the acoustic time and the time of pressure oscillation amplitude variation. These time scales differ by approximately three orders of magnitude, which demands high computational accuracy. A simpler solution method is developed in the quadratic approximation with respect to the amplitude of oscillations. This method accounts only for the effects related to the time scale of oscillation amplitude variation. Numerical results are obtained for the simplest propellant combustion model in the absence of entropic waves in combustion products. Stable and unstable combustion regimes are identified. In the latter regime, nonlinear effects may trigger shock waves in the combustion chamber.

The possibility of expanding the theory beyond the phenomenological framework is discussed in the final chapter. This development requires a more detailed combustion model that would adequately describe processes occurring in low‐inertia zones of a combustion wave. The influence of low‐inertia zones (the reacting layer of the condensed phase, preheat and reaction zones in the gas phase, the half‐space occupied by gaseous combustion products) on various nonsteady phenomena are investigated both analytically and numerically. The consideration is presented within the framework of the Belyaev model. It is demonstrated that under a weak dependence of surface temperature on initial temperature accounting for the above low‐inertia zones (even if their thermal inertia is small compared to the inertia of the preheat layer of the condensed phase) leads to significant corrections to the t capproximation.

Finally, it is our pleasure to acknowledge the significant contribution of the people who helped us in the preparation of this book.

We are very grateful to Professor Vladimir Marshakov, who discussed various topics throughout the book with us at great length.

Special thanks are given to Inga Novozhilov. It is certain that without her very careful and dedicated work the manuscript could not have been adequately prepared.

We are also incredibly thankful to Professor Vladimir Posvyanskii, Ludmila Novozhilova, and Natalia Golubnichaya for their help in preparing the manuscript.

The second author would like to thank his wife Natalia Golubnichaya again for her love and continuous support throughout the project.

Moscow – Belfast – Melbourne

2011–2019

Boris V. Novozhilov Vasily B. Novozhilov

Over‐bar complex conjugate; Laplace–Carson transform

prime	time derivative, case‐specific dimension; perturbed value, case‐specific dimension
Basic Physical Dimensions	M (mass), L (length), T (time), θ (temperature), N (amount of substance, e.g. mole)
a	speed of sound, LT −1; amplitude, case‐specific dimension
a f	amplitude of forced oscillations, case‐specific dimension
A	nozzle discharge coefficient, L −1 T
b	combustion temperature, nondimensional; correction (Chapter 9)
c	specific heat at constant volume, L 2 T −2 θ −1
c p	specific heat at constant pressure, L 2 T −2 θ −1
D , D g	gas diffusion coefficient, L 2 T −1; amplitude of perturbation (Chapter 3), L ; integration constant, nondimensional (Chapter 9)
E	activation energy, ML 2 T −2 N −1
f	temperature gradient at the surface, condensed phase side, θL −1
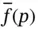	Laplace–Carson transform of f ( t ), case‐specific dimension
J	Jacobian, L 2 M −1 T
g	mass velocity of gas flow, ML −2 T −1
G	response function of gas velocity to oscillating pressure, non‐dimensional; integration constant, nondimensional (Chapter 9)
h	amplitude of perturbation of relative pressure, nondimensional
I	radiative heat flux, MT −3
k	sensitivity coefficient, nondimensional
K	distortion factor, nondimensional; burning rate amplification coefficient, nondimensional; wave vector, L −1
l	thickness of thermal layer of the condensed phase, L ; mean free path for radiation absorption in the condensed phase, nondimensional
l b	distance away from surface at which heat generation becomes negligible
L	length of cylindrical combustion chamber, L ; latent heat of evaporation, L 2 T −2
m	mass burning rate, ML −2 T −1
m g	mass velocity of the gas stream, ML −2 T −1
M	Mach number, nondimensional; mass of gas in the chamber, M
p	pressure, ML −1 T −2
q	heat flux into the condensed phase, MT −3
Q = Q s+ Q g	total heat of combustion/reaction, L 2 T −2
Q g	heat of combustion/reaction in the gas phase, L 2 T −2
Q s	heat of reaction in the condensed phase, L 2 T −2
r	sensitivity parameter, nondimensional
r b	sensitivity parameter, nondimensional
R	Universal gas constant, ML 2 T −2 θ −1 N −1
s	relative change of the nozzle cross‐sectional area, nondimensional; correction (Chapter 9), nondimensional; surface temperature in the steady‐state regime at initial pressure (Chapter 9), nondimensional
S	cross‐sectional area of cylindrical combustion chamber, L 2
t	time, T
T	temperature, θ ; period of oscillations, nondimensional
T k	reference temperature (Chapter 7), θ
u	propellant linear burning rate, LT −1
u g	dimensional gas velocity normal to the surface, LT −1
u p	gas velocity normal to the surface in the combustion products zone (Belyaev model), LT −1
U	response function of burning rate to oscillating pressure, non‐dimensional; mass burning rate dependence on temperature and pressure (Chapter 9), ML −2 T −1
v	propellant linear burning rate, nondimensional
v g	gas velocity normal to the surface, nondimensional
v p	gas velocity normal to the surface in the combustion products zone (Belyaev model), nondimensional
V	volume of combustion chamber, L 3
w	tangential gas velocity, LT −1
w t	tangential gas velocity, nondimensional
W	chemical reaction rate, ML −3 T −1
x	cartesian coordinate, L
y	cartesian coordinate, L , or nondimensional; correction (Chapter 9), nondimensional
Y	reactant mass fraction, nondimensional