They concluded by affirming that
It can be fairly stated that there is no form of evidence whose interpretation is so definite that statistical treatment is not needed or desirable. (p. 437)
As discussed in Section 1.2, there have been several books describing the role of statistics in the law. Until the first edition of this book, there had been none concerned with statistics and the evaluation of scientific evidence. Two factors may have been responsible for this.
First, there was a lack of suitable data from relevant populations. There was a consequential lack of a baseline against which measures of typicality of any characteristics of interest may be determined. One exception are the reference data that have been available for many years on allele frequencies for DNA analysis amongst certain populations. Not only has it been possible to say that the DNA of a PoI corresponded 4 to that of a stain found at the scene of a crime, but also that this profile is only present in, say, 0.01% of the population. Now these have been superceded by results of surveys of allele frequencies in various populations. Announcements of population data are published regularly in peer‐reviewed journals such as Forensic Science International: Genetics and the International Journal of Legal Medicine . Also, data collections exist for the refractive index of glass fragments found at random on clothing and for transfer and persistence parameters linked to glass evidence; see, for example, Curran et al. (2000), O'Sullivan et al. (2011), and Jackson et al. (2013). Contributions towards characterising the rarity of different fibre types have also been published since the late 1990s; for a review, see Palmer (2016).
Secondly, the approach adopted by forensic scientists in the assessment of their evidence has been difficult to model. The approach has been one of comparison and significance. Characteristics of the control and recovered items are compared. If the examining scientists believe them to be similar, the typicality, and hence the significance of the similarity, of the characteristics is then assessed. This approach is what has been modelled by the two‐stage approach of Evett (1977), described briefly in Section 1.3.3and in fuller detail in Chapter 3. However, interpretation of the results provided by this approach is difficult.
Then, in a classic paper, Lindley (1977c) described an approach that was easy to justify, to implement, and to interpret. It combined the two parts of the two‐stage approach into one statistic and is discussed in detail in Section 7.4.3. The approach compares two probabilities, the probability of the evidence, assuming one proposition to be true (e.g. that a PoI is the source of the evidence), and the probability of the evidence, assuming another, mutually exclusive, proposition to be true (e.g. that the PoI is not the source of the evidence). Note that some people use the term hypothesis rather than proposition ; the authors will endeavour to use the term proposition as they believe this reduces the risk of confusion of their ideas with the ideas of hypothesis testing associated with the alternative term. A proposition is interpreted here as an assertion or statement that, for example, a particular outcome has occurred or a particular state of nature occurs.
This approach implies that it is not enough for a prosecutor to show that there is a low probability to observe the evidence if a PoI is innocent. It should also be more probable to observe the evidence if the PoI is truly guilty. Such an approach has a good historical pedigree (Good, 1950, and also Good, 1991, for a review) yet it had received very little attention in the forensic science literature, even though it was clearly proposed at the beginning of the twentieth century (Taroni et al. 1998; Champod et al. 1999), and earlier by Peirce (1878). It is also capable of extension beyond the particular type of example discussed by Lindley, as will be seen by the discussion throughout this book, for example, in Chapters 6and 7.
However, in order to proceed it is necessary to have some idea about how uncertainty can be measured. This is best done through probability (Lindley 1991, 1985, 2014). This central role for probability in evidence evaluation is supported by the ENFSI. In the ENFSI Guideline for evaluative reporting in forensic science, 5 is reported, at page 6 (under point 2.3), that:
Evaluation of forensic science findings in court uses probability as a measure of uncertainty. This is based upon the findings, associated data and expert knowledge, case specific propositions and conditioning information.
where the term ‘findings’ denotes ‘evidence’ in our usage.
1.7.2 A Standard for Uncertainty
An excellent description of probability and its role in forensic science has been given by Lindley (1991). Lindley's description starts with the idea of a standard for uncertainty. He provides an analogy using the concept of balls in an urn. Initially, the balls are of two different colours, black and white. In all other respects, size, weight, texture, etc., they are identical. In particular, if one were to pick a ball from the urn, without looking at its colour, it would not be possible to tell what colour it was. The two colours of balls are in the urn in proportions 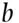 and
and 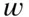 for black and white balls, respectively, such that
for black and white balls, respectively, such that 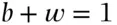 . For example, if there were 10 balls in the urn of which 6 were black and 4 were white, then
. For example, if there were 10 balls in the urn of which 6 were black and 4 were white, then 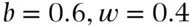 , and
, and 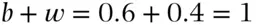 .
.
The urn is shaken up and the balls thoroughly mixed. A ball is then drawn from the urn. Because of the shaking and mixing, it is assumed that each ball, regardless of colour, is equally likely to be selected. Such a selection process, in which each ball is equally likely to be selected, is known as a random selection, and the chosen ball is said to have been chosen at random .
The ball, chosen at random, can be either black, an event that will be denoted 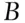 , or white, an event that will be denoted
, or white, an event that will be denoted 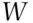 . There are no other possibilities; one and only one of these two events has to occur. The uncertainty of the event
. There are no other possibilities; one and only one of these two events has to occur. The uncertainty of the event 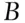 , the drawing of a black ball, is related to the proportion
, the drawing of a black ball, is related to the proportion 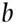 of black balls in the urn. If
of black balls in the urn. If 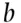 is small (close to zero),
is small (close to zero), 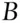 is unlikely. If
is unlikely. If 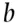 is large (close to 1),
is large (close to 1), 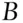 is likely. A proportion
is likely. A proportion 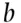 close to 1/2 implies that
close to 1/2 implies that 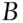 and
and 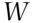 are about equally likely. The proportion
are about equally likely. The proportion 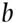 is referred to as the probability of obtaining a black ball on a single random drawing from the urn. In a similar way, the proportion
is referred to as the probability of obtaining a black ball on a single random drawing from the urn. In a similar way, the proportion 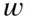 is referred to as the probability of obtaining a white ball on a single random drawing from the urn.
is referred to as the probability of obtaining a white ball on a single random drawing from the urn.
Читать дальше

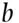 and
and 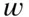 for black and white balls, respectively, such that
for black and white balls, respectively, such that 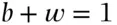 . For example, if there were 10 balls in the urn of which 6 were black and 4 were white, then
. For example, if there were 10 balls in the urn of which 6 were black and 4 were white, then 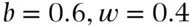 , and
, and 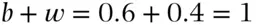 .
.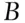 , or white, an event that will be denoted
, or white, an event that will be denoted 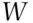 . There are no other possibilities; one and only one of these two events has to occur. The uncertainty of the event
. There are no other possibilities; one and only one of these two events has to occur. The uncertainty of the event 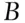 , the drawing of a black ball, is related to the proportion
, the drawing of a black ball, is related to the proportion 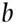 of black balls in the urn. If
of black balls in the urn. If 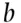 is small (close to zero),
is small (close to zero), 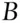 is unlikely. If
is unlikely. If 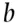 is large (close to 1),
is large (close to 1), 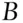 is likely. A proportion
is likely. A proportion 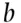 close to 1/2 implies that
close to 1/2 implies that 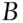 and
and 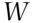 are about equally likely. The proportion
are about equally likely. The proportion 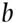 is referred to as the probability of obtaining a black ball on a single random drawing from the urn. In a similar way, the proportion
is referred to as the probability of obtaining a black ball on a single random drawing from the urn. In a similar way, the proportion 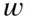 is referred to as the probability of obtaining a white ball on a single random drawing from the urn.
is referred to as the probability of obtaining a white ball on a single random drawing from the urn.










