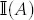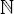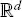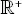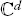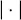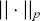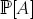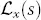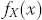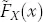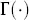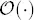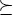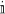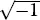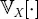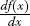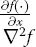Hirley Alves - Wireless RF Energy Transfer in the Massive IoT Era

230 212

231 213

232 214

233 215

234 216

235 217

236 218

237 219

238 220

239 221

240 222

241 223

242 224

243 225

244 226

245 227

246 228

247 229

248 230

249 231

Even though there is vast literature on radio-frequency energy harvesting and wireless energy transfer, the majority of the works do not focus on Internet of Things network deployments and their inherent characteristics and stringent requirements, particularly, the need to support the operation of a massive number of low-power low-cost devices. Powering this massive number of devices is challenging and cannot be done by adapting conventional models designed for a limited number of users. Massive Internet of Things networks will connect thousands to millions of devices in a single cell.

The lack of dedicated solutions prompted us to research in this area, which we call “massive wireless energy transfer” (massive WET). We then decided to gather the most recent contributions on massive radio frequency energy harvesting and compile the information into a single reference that can serve as a guide for future research in this revitalized area. This book reviews the state-of-the-art in radio frequency energy harvesting and points out future research directions. A basic background in statistics and wireless communications is sufficient to read this book, while some basic knowledge of linear algebra, convex optimization, and statistical signal processing may be needed to thoroughly follow the main theoretical derivations and analysis.

The book is divided into eight chapters. In a nutshell, Chapter 1and Chapter 2introduce the key concepts and provide an overview of the energy harvesting technologies in the context of massive networks. Then, Chapters 3to 7delve into analytical and algorithmic aspects of the different protocols, techniques, and scenarios examined in each chapter. Finally, Chapter 8summarizes the key contributions of each chapter and indicates future research directions.

In Chapter 1, we overview the concept of massive IoT and related connectivity components. Chapter 2is an overview of the energy harvesting technology based on radio frequency energy transfer for powering future low-power massive network deployments. In Chapter 3, we focus on ambient radio frequency energy harvesting techniques, which exploit readily available environmental radio frequency energy, and review key protocols and scenarios. Then, in Chapter 4, we delve into massive wireless energy transfer, in which energy transmissions from dedicated energy sources energize a massive number of energy harvesting devices, and propose novel energy transfer mechanisms tailored for massive Internet of Things networks. In Chapter 5, we concentrate on a network of power beacons, which are dedicated radio frequency energy transmitter devices. Therein, we discuss and propose optimization approaches for the deployment of a network of power beacons. Next, Chapter 6discusses the wireless-powered communication network architecture, key characteristics, protocols, and single and multi-user scenarios with respective power control strategies. Chapter 7overviews the simultaneous wireless information and power transfer architecture, the main receivers, and representative scenarios. Finally, Chapter 8summarizes the key contributions of this book and indicates future research directions.

Researchers who want to delve into the field of radio frequency energy harvesting can read this book from cover to cover. Chapter 1provides the motivation and introduction to general ideas discussed in the book. Chapter 2is instrumental to understanding the underlying analytical models used in the remaining chapters. Therefore, after reading Chapter 2, Chapters 3, 4, 6and 7can be read in any order, based on personal preference. Even though Chapter 5can be read independently, it relies on concepts introduced in Chapter 4.

Each chapter ends with a summary of the key points and contributions. A researcher familiar with the broad field of radio frequency energy harvesting can read the summary and become acquainted with the content, and then decide to read in detail.

Onel Alcaraz López and Hirley Alves

Oulu, May 2021

We are thankful to our colleagues, collaborators, friends, and family for their constant support and encouraging words throughout the writing of this book.

We thank Richard Demo Souza and Samuel Montejo Sánchez for their detailed comments and insightful ideas. These discussions kept us pushing toward further exploration of our research both in breadth and depth.

We thank Pedro H. J. Nardelli, Dick Carrillo Melgarejo, Nelson J. Mayedo Rodríguez, Dian Echevarría Pérez, Osmel M. Rosabal, Jean de Souza Sant’Ana, Richard Demo Souza and Samuel Montejo Sánchez for their valuable feedback on specific chapters.

We thank Sarah Lemore (Associate Managing Editor, Wiley) for the assistance provided and for putting up with our requests for extensions, which were granted and all were duly appreciated and well used.

We thank our families for their patience, support, and occasionally taking the blame for our lack of skills in time management. Even then, they were always there for us.

O. A. L. & H. A.

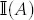	indicator function. It is equal to 1(0) if A is true(false)
[ x ] +	max( x ,0)
[ x ] ×	min( x ]+, ref ), where ref refers to certain reference level according to the application scenario, e.g., Bmax
~	distributed as
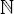	set of natural numbers
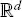	real coordinate space of dimension is omitted when equals to 1
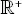	set ofpositive real numbers
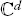	complex coordinate space ofdimension d. d is omitted when equals to 1
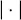	denotes cardinality or absolute value operation in case of a set or a scalar as input, respectively
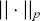	lp norm. The value ofp may or may not be specified when p = 2 expected value with respect to random variable X. When X is not specified, the expected value is with respect to all random variables
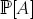	probability of occurrence of event A
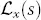	Laplace transform of random variable X
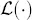	inverse Laplace transform operator
fX ( x )	PDF of random variable X
FX ( x )	CDF of random variable X
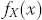	CCDF of random variable X
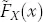	gamma function
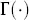	upper incomplete gamma function
Kv(·)	modified Bessel function of the second kind and order v
erf(·)	error function
Tr(·)	matrix trace operator
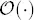	big-O notation
diag(x)	diagonal matrix with the main diagonal from entries of x
(·) T	transpose operator
(·) H	Hermitian transpose operator
rank(·)	rank operator
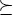	generalized greater-than-or-equal-to inequality: between vectors, it represents component-wise inequality; between symmetric matrices, it represents matrix inequality
inf ·	infimum operator
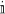	imaginary unit, i.e.,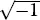
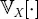	variance with respect to random variable X. When X is not specified, the variance is with respect to all random variables
Jn (·)	Besselfunction of first kind and order n
det(·)	determinant operation
mod( a , b )	a modulo b operation
atan2( c )	returns the angle in the Euclidean plane between the positive x axis and the ray to the point c
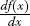	derivative ofsingle-variable function f
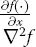	partial derivative ofmulti-variable function f with respect to x Hessian offunction f
Q(·)	Q-function, the tail distribution function of the standard normal distribution

Distributions