Кроме письма, на заре цивилизации появились и записи чисел . Сегодня математики различают числа , которые представляют собой абстрактные сущности, и их запись – некие физические символы для представления чисел. Первыми были открыты именно они. Сначала считали с помощью «черточек» (|,||,|||,||||, …) или счетных единиц, например, камней, которые с доисторических времен использовались для учета таких дискретных сущностей, как животные или дни [29]. Если каждую выпущенную из загона козу отмечать черточкой, а потом, когда коза возвращается, ее перечеркивать, то когда все черточки окажутся перечеркнутыми, это будет означать, что все козы на месте.
Это универсальная система счета. Но, аналогично уровням эмерджентности, у универсальности тоже есть иерархия. Следующий уровень после счета «палочками» – счет, в котором задействована специальная запись числа. В первом случае, отмечая, сколько коз пришло или ушло, человек думает просто «еще одна, еще одна и еще одна», а считая их, он проговаривает про себя «сорок, сорок одна, сорок две…».
Только задним числом мы можем рассматривать «палочки» как систему счисления и называть ее «унарной» («единичной»), и как таковая эта система непрактична. Например, даже простейшие операции с числами, представленными черточками, такие как сравнение, арифметические операции и даже просто копирование, влекут за собой повторение всего процесса. Если у вас было сорок коз, вы продали двадцать и отметили оба этих действия с помощью черточек, вам все равно придется произвести двадцать отдельных операций удаления, чтобы записи соответствовали действительности. Аналогично, чтобы проверить, совпадают ли две сходные на вид записи, пришлось бы вычерчивать их друг под другом и сличать. Поэтому люди начали совершенствовать систему. Наверно, раньше всего придумали просто группировать черточки – например, писать  вместо ||||||||||. Так сравнивать числа и проводить арифметические операции стало проще, поскольку можно было записывать целые группы и сразу видеть, что
вместо ||||||||||. Так сравнивать числа и проводить арифметические операции стало проще, поскольку можно было записывать целые группы и сразу видеть, что  отличается от
отличается от 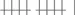 . Позднее и для самих этих групп были подобраны более короткие условные символы: в древнеримской системе использовались символы типа I, V, X,
. Позднее и для самих этих групп были подобраны более короткие условные символы: в древнеримской системе использовались символы типа I, V, X, 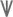 , C, D, и CD для обозначения одного, пяти, десяти, пятидесяти, сотни, пяти сотен и тысячи. (Как видите, это не совсем те «римские цифры», которые мы используем сегодня.)
, C, D, и CD для обозначения одного, пяти, десяти, пятидесяти, сотни, пяти сотен и тысячи. (Как видите, это не совсем те «римские цифры», которые мы используем сегодня.)
Это еще один случай постепенного совершенствования, направленного на решение специфических, обывательских проблем. И снова, по-видимому, никто к большему и не стремился. Хотя добавлением простых правил можно было сделать систему гораздо более функциональной, и даже несмотря на то, что римляне действительно время от времени добавляли некоторые из таких правил, они делали это, не стремясь к универсальности и не достигая ее. На протяжении нескольких столетий в этой системе правила были следующие.
– Размещенные рядом символы складываются. (Это правило унаследовано от системы подсчета «палочек».)
– Символы записываются слева направо в порядке убывания их величины.
– Когда это возможно, смежные символы следует заменять одним, отражающим их суммарное значение.
(Правило вычитания, присутствующее в современной римской системе счисления, по которому IV означает четыре, было введено позже.) Второе и третье правило гарантируют единственность представления каждого числа, что сильно упрощает сравнение. Без этих правил могли бы существовать и XIXIXIXIXIX, и VXVXVXVXV, и никто не мог бы с первого взгляда сказать, что это одно и то же число.
За счет применения универсальных законов сложения эти правила давали системе одно важное преимущество над подсчетом с помощью «палочек», а именно возможность производить арифметические операции. Например, возьмем числа семь (VII) и восемь (VIII). Согласно правилам поместить их друг за другом VIIVIII – все равно что сложить их. Затем по правилам нужно переставить символы в порядке убывания их величины: VVIIIII. Затем нужно заменить две V на X и пять I на V. В результате получим XV, что является представлением числа пятнадцать. Но при этом происходит нечто новое, и дело не просто в сокращении записи: открыта и доказана абстрактная истина, связывающая между собой семь, восемь и пятнадцать, и при этом никто ничего не отмечал и не пересчитывал. Мы работали с самими числами, посредством их записей.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

 вместо ||||||||||. Так сравнивать числа и проводить арифметические операции стало проще, поскольку можно было записывать целые группы и сразу видеть, что
вместо ||||||||||. Так сравнивать числа и проводить арифметические операции стало проще, поскольку можно было записывать целые группы и сразу видеть, что  отличается от
отличается от 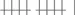 . Позднее и для самих этих групп были подобраны более короткие условные символы: в древнеримской системе использовались символы типа I, V, X,
. Позднее и для самих этих групп были подобраны более короткие условные символы: в древнеримской системе использовались символы типа I, V, X, 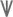 , C, D, и CD для обозначения одного, пяти, десяти, пятидесяти, сотни, пяти сотен и тысячи. (Как видите, это не совсем те «римские цифры», которые мы используем сегодня.)
, C, D, и CD для обозначения одного, пяти, десяти, пятидесяти, сотни, пяти сотен и тысячи. (Как видите, это не совсем те «римские цифры», которые мы используем сегодня.)










