Array Журнал «Искатель» - Искатель, 1961 №6

Рисунки Э. Рогова

Перед диспетчером лежала пачка бумаг — двести с лишним заявок от различных строек Москвы. Все заявки были на строительный песок. Диспетчер знал, что песок вывозится с восьми речных пристаней, знал их расположение, состояние автопарка и количество автомашин. Ему нужно было спланировать работу этих автомашин, спланировать наиболее рационально.

Теперь попробуйте решить такую задачу. На схеме показан участок железнодорожной сети и расстояния в километрах между станциями. На станциях А и Г находится соответственно по 300 и 200 тонн груза. На станцию Б надо доставить 300 и В — 200 тонн груза. Необходимо определить, как везти груз (то есть как прикрепить пункты производства к пунктам потребления), чтобы общий пробег груза был минимальным. На первый взгляд наиболее правильно было бы везти груз из А в Б, а на станцию В доставлять груз из Г. Пробег груза при таком прикреплении составит: 300 т x 80 км + 200 т x 20 км=28 000 тонна-километров. Попробуем теперь прикрепить В к А, а Б к пунктам Г и А. В этом случае перевозочная работа будет равна 200 т х30 км + 100 т х 80 км + 200 т x 40 км = 26 000 тонна-километров. Таким образом, второй план перевозки уменьшает пробег груза более чем на 7 процентов. Он, конечно, лучше, чем первый, не так ли?

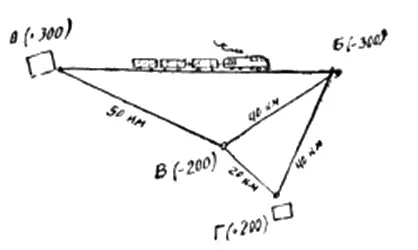
Вот видите, даже в такой простой задаче можно легко ошибиться!

А теперь снова заглянем в контору нашего диспетчера.

Если бы он попробовал перебрать все возможные варианты, как это было сделано в предыдущей задаче, то число их составило бы астрономическую цифру, приближенно равную единице с двумястами нулями. Даже на электронной вычислительной машине (ЭВМ) с ее огромным быстродействием такой расчет занял бы несколько суток!

Но задача была решена за один час. Как? Методом линейного программирования на электронной машине «Стрела».

И хотите знать результат? Составленный план, обеспечивая нужды всех строек, уменьшал пробег автомобилей на 11,5 процента по сравнению с тем планом, который удалось составить диспетчеру без вычислительной машины.

Линейное программирование — это новая отрасль математики, тесно связанная с использованием электронных вычислительных машин. Методы линейного программирования при решении задачи позволяют не перебирать все варианты — вот в чем их неоценимое достоинство.

Еще два примера.

Основной вид газетной бумаги доставляется по железным дорогам с 6 комбинатов в 112 издательств. Рассчитанный на ЭВМ менее чем за час оптимальный план сокращал величину перевозки на 2,67 миллиона тонна-километров по сравнению с действующим планом!

Надо было составить план расстановки различного типа судов речного флота с тем, чтобы обеспечить максимальный объем перевозок с минимальными расходами. Результаты решения этой конкретной задачи на ЭВМ оказались весьма обещающими: кибернетическая машина, получив запрограммированные исходные данные, составила план, при котором коэффициент использования грузоподъемности судов увеличивался на 30 процентов…

Что показывают такие исследования? Рассчитано, что при помощи ЭВМ и методов линейного программирования существующие планы перевозок можно улучшить: их эффективность возрастет на 5-15 процентов. И когда наиболее рациональные схемы перевозок будут применены, причем в масштабах всего народного хозяйства, мы ежегодно будем экономить миллиарды рублей!

Сейчас разрабатываются методы линейного программирования для того, чтобы планировать наилучшее размещение новых производственных предприятий, заводов и фабрик. Эта проблема имеет огромную государственную важность.

Ведь направление перевозок и размещение производства взаимно влияют друг на друга. Учитывая это, и надо решать задачу, где и как строить. Исходными данными для решения такой комплексной задачи будут допустимые минимальные и максимальные объемы производства каждого предприятия и стоимости перевозки продукции к местам потребления. В результате можно определить размеры производства для каждого заданного пункта. Причем это будут размеры, которые при полном удовлетворении нужд потребления обеспечат минимум затрат на производство и перевозку продукции потребителям.