Array Сборник - Интеллектуальная энергетика

Тюрина Наталья Александровна, turinanatalie@yandex.ru

Грибанов Алексей Александрович, diread@mail.ru

Аннотация:

В статье подробно рассмотрен метод регрессионного моделирования для формирования математической модели расчета для последующего расчета удельной мощности для проектирования освещения в помещениях промышленного и общественного назначений. Также в статье представлен подробный расчет относительной погрешности модели.

Ключевые слова:метод удельной мощности, математическая модель, регрессионное моделирование, освещенность, источники света.

Расчет электрических нагрузок является основополагающим этапом проектирования систем электроснабжения. Электрические нагрузки подразделяются на силовые и осветительные. На сегодняшний день существуют три наиболее популярных метода расчета осветительных нагрузок: метод удельной мощности, точечный метод, метод коэффициента использования. Метод удельной мощности наиболее часто используется проектировщиками для приближенного расчета мощности осветительного оборудования, отличается простотой использования и сравнительно малым объемом исходных данных, что значительно расширяет круг его использования. Значения удельной мощности были получены в середине двадцатого столетия и, к сожалению, их использование для современных светодиодных и люминесцентных источников некорректно[1]. В ходе эксперимента мною были получены актуальные значения для таких источников.

В рамках исследования было проведено 830 экспериментов путем расчета в среде Dialux evo, рассмотрено 29 расчетных случаев. Расчетный случай – это помещение общественного и промышленного назначения, для которых определялись нормируемая освещенность, высота подвеса источников света, площадь. Помимо этого, для каждого расчетного случая было отобрано 6 источников света. Всего в эксперименте участвовало 49 источников света.

В ходе исследования были получены математические модели, для каждой из которых посчитаны относительная погрешность источника света и относительная погрешность для расчетного случая. Значения относительных погрешностей лежат в допустимом диапазоне, что позволяет в дальнейшем рассчитывать мощность источников света для проектирования освещения в помещениях промышленного и общественного назначений для входных параметров, не участвовавших в эксперименте.

Общий вид математической модели (1):

𝑊=𝑎∙𝑆 4+𝑏∙𝐸 4+𝑐∙𝑆 3+𝑑∙𝐸 3+𝑒∙𝑆 3𝐸+𝑓∙𝑆 3𝐻 𝑝+𝑔∙𝐸 3𝐻 𝑝+ℎ∙

𝐸 3𝑆+𝑖∙𝐻 𝑝 2+𝑗∙𝑆 2+𝑘∙𝐸 2+𝑙∙𝐻 𝑝 2𝑆+𝑚∙𝐻 𝑝 2𝑆 2+𝑛∙𝐻 𝑝 2𝐸 2+𝑜∙𝑆 2𝐸 2+𝑝∙

𝐻 𝑝 2𝐸+𝑞∙𝑆 2𝐻 𝑝+𝑟∙𝑆 2𝐸+𝑠∙𝐸 2𝑆+𝑡∙𝐸 2𝐻 𝑝+𝑢∙𝐻 𝑝 2∙𝑆∙𝐸+𝑣∙𝐻 𝑝∙𝑆 2∙𝐸+

𝑤∙𝐻 𝑝∙𝑆∙𝐸 2+𝑥∙𝐻 𝑝+𝑦∙𝑆+𝑧∙𝐸+𝛼∙𝐻 𝑝∙𝑆+𝛽∙𝐻 𝑝∙𝐸+γ∙𝑆∙𝐸+𝛿∙𝐻 𝑝∙𝑆+𝜀

(1)

где – значение удельной мощности осветительной нагрузки на единицу площади помещения, Вт/м 2;

a, b, c, d, e, f, g, h, i, j,k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, 𝛼,𝛽,γ,𝛿,𝜀 – коэффициенты регрессионного уравнения, которые необходимо определить.

Для определения значения уровня варьирования применялась следующая формула (2):

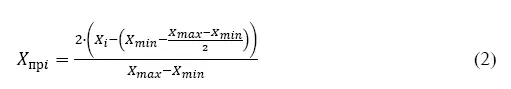
где 𝑋 пр𝑖– значение параметра, приведённое к шкале от −1 до +1;

𝑋 𝑖– текущее значение параметра, абс. ед.;

𝑋 𝑚𝑎𝑥– максимальное значение параметра, абс. ед.;

𝑋 𝑚𝑖𝑛– минимальное значение параметра, абс. ед.

Уровни варьирования для использовавшихся в экспериментах параметров ниже приведены в таблице 1.

Таблица 1

Уровни варьирования параметров

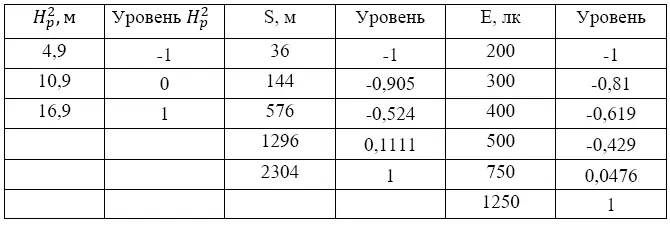
Для определения коэффициентов уравнения приведем результаты расчётного эксперимента к табличному виду. В дальнейших таблицах для упрощения введён параметр X 0=1, соответствующий свободной переменной, перед которой стоит коэффициент.

Данные эксперимента для источника света ULV-R24J представлены в таблице 2.

Таблица 2

Таблица эксперимента для источника света ULV-R24J

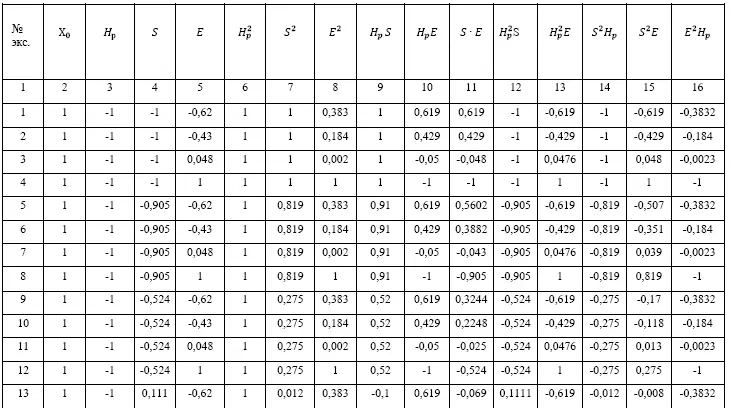
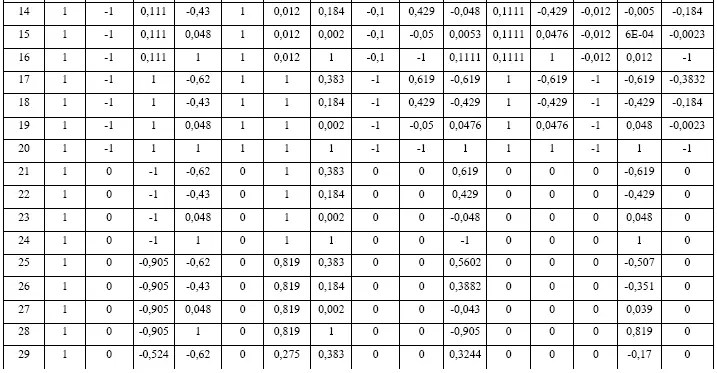
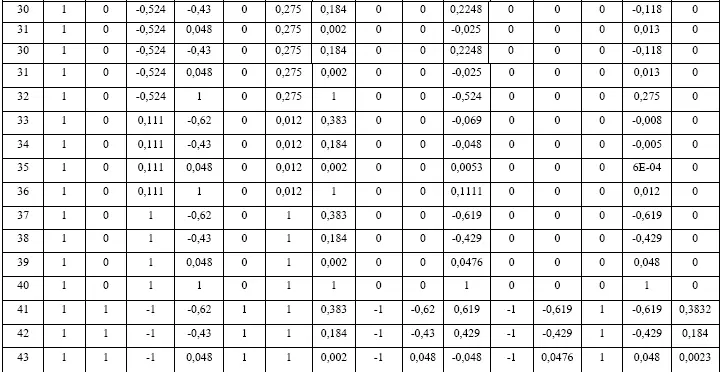
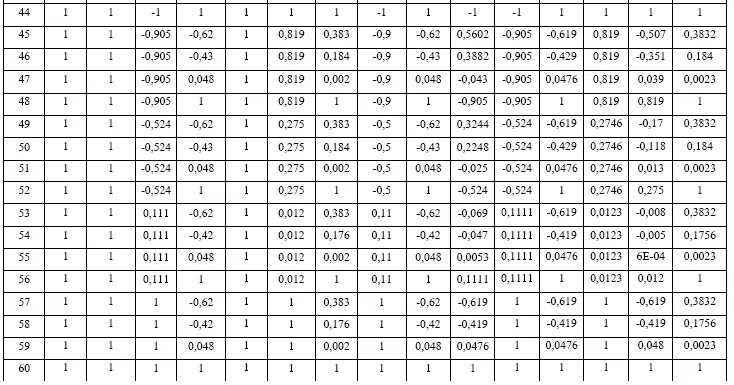
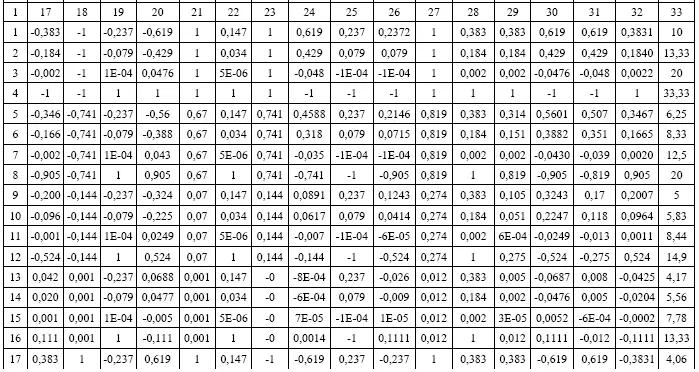
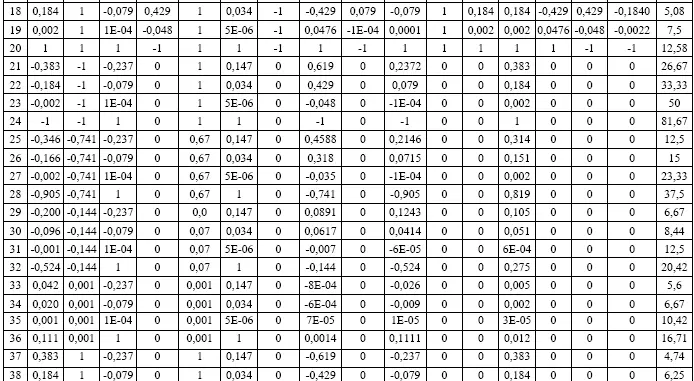
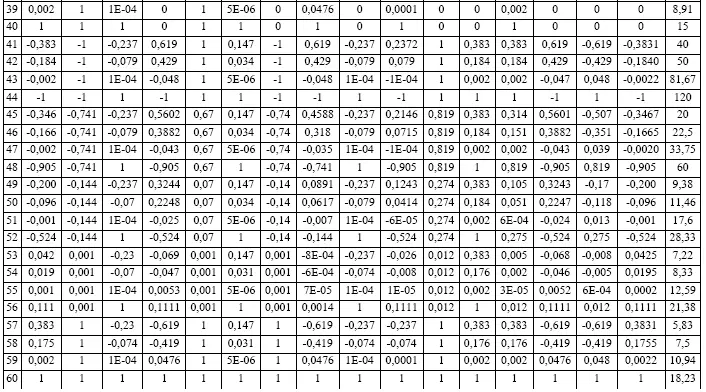
Для определения коэффициентов уравнения была составлена матрица Х, включающая в себя закодированные условия эксперимента (столбцы 2-32 таблицы 2) и матрица Y, включающая в себя результаты эксперимента (столбец 33 таблицы 2). Далее матрица Х транспонируется и умножается на исходную матрицу Х, получается матрица X т·X. Матрица Y также умножается на транспонированную матрицу X, получается матрица X т·Y. Затем для матрицы X т·X вычисляется обратная матрица матрицы X т·X -1. Перемножив обратную матрицу X т·X -1и матрицу X т·Y получим матрицу коэффициентов уравнения. Аналогичные действия были проведены и для других источников. Коэффициенты уравнения представлены в таблице 3.