Стефан Дэвис - С++ для чайников .

[ Атас! ]

Разложение может давать ( и обычно даёт ) результат на нескольких уровнях абстракции. Например, программа, написанная для более "продвинутого" банка, может иметь структуру классов, показанную на рис. 22.4.

Из этого рисунка видно, что между классами Checking и Savings и более общим классом Account вставлен ещё один класс. Он называется Conventional и объединяет в себе особенности обычных счетов. Другие типы счетов, например счета ценных бумаг и биржевые счета, также объявляются как отдельные классы.

Такая многослойная структура классов весьма распространена и даже желательна ( пока отношения, которые она представляет, отражают реальность. Однако не забывайте, что для любого заданного набора классов не существует одной единственно правильной иерархии классов ).

_________________

252 стр. Часть 4. Наследование

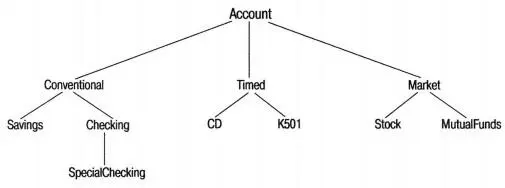
Рис. 22.4. Развитая структура банковских счетов

Представим, что банк позволяет держателям счетов удаленно обращаться к чековым счетам и счетам ценных бумаг. Снимать же деньги с других типов счетов можно только в банке. Хотя структура классов, приведённая на рис. 22.4, выглядит естественной, в данных условиях более приемлема другая структура ( рис. 22.5 ). Программист должен решить, какая структура классов лучше всего подходит к данным условиям, и стремиться к наиболее ясному и естественному представлению.

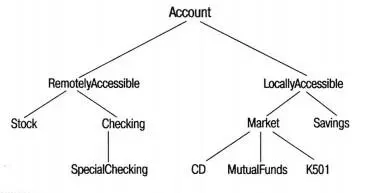
Рис. 22.5. Альтернативная иерархия классов

Такое интеллектуальное упражнение, как разложение, поднимает ещё одну проблему. Вернёмся к классам банковских счетов ещё раз, а именно к общему базовому классу Account . На минуту задумайтесь над тем, как вы будете определять различные функции класса Account .

Большинство функций-членов класса Account не составят проблем, поскольку оба типа счетов реализуют их одинаково. Однако функция Account.withdrawal( ) отличается в зависимости от типа счёта. Правила снятия со сберегательного и чекового счетов различны. Мы вынуждены реализовывать Savings::withdrawal( ) не так, как Checking::withdrawal( ) . Но как реализовать функцию Account::withdrawal( ) ?

Попросим банковского служащего помочь нам. Я так представляю себе эту беседу:

"Каковы правила снятия денег со счёта?" — спросите вы с надеждой.

"Какого именно счёта, сберегательного или чекового?" — ответит он вопросом на вопрос.

"Со счёта, — скажете вы, — просто со счёта!"

_________________

253 стр. Глава 22. Разложение классов

Пустой взгляд в ответ...

Проблема в том, что такой вопрос не имеет смысла. Нет такой вещи, как "просто счёт". Все счета ( в данном примере ) должны быть чековыми или сберегательными. Концепция счёта — это абстракция, с помощью которой мы объединяем общие свойства для конкретных счетов. Это незавершённая концепция, поскольку в ней отсутствует такое важное свойство, как функции withdrawal( ) ( если вы углубитесь в детали, то найдёте и другие свойства, которых не хватает "просто счёту" ).

Абстрактный класс — это тот класс, который реализуется только в подклассе. Конкретный — тот, который не является абстрактным.

Чтобы объяснить, что я имею в виду, позвольте позаимствовать пример из мира животных. Наблюдая разные особи теплокровных и живородящих, вы можете заключить, что они все укладываются в концепцию под названием "млекопитающие". Вы можете выделить такие классы млекопитающих, как собачьи, кошачьи и приматы. Однако невозможно найти где-либо на земле просто млекопитающее. Другими словами, млекопитающие не могут содержать особь под названием "млекопитающее". Млекопитающее — это концепция высокого уровня, которую создал человек, и экземпляров-млекопитающих не существует.

Обратите внимание, что утверждать это с уверенностью я могу только по истечении некоторого времени. Ученые постоянно открывают новые виды животных. Проблема в том, что каждое существо обладает свойствами, которых не имеют другие; однако вполне вероятно, что в будущем кто-то найдёт такое свойство у других существ.

Отражая эту ситуацию, С++ даёт возможность оставлять абстрактные классы незавершёнными.

Абстрактный класс — это класс с одной или несколькими чисто виртуальными функциями. Прекрасно, это всё разъясняет...