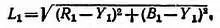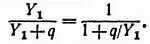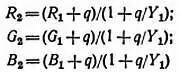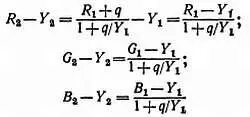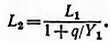Евгений Айсберг - Цветное телевидение?.. Это почти просто!

Можно также отметить, что

R— Y= -0,59 G+ 0,70 R— 0,11 B;

B— Y= -0,59 G— 0,30 R + 0,89 B.

тогда как

G— Y= -0,41 G— 0,30 R— 0,11 B

Рассматривая приведенные равенства, констатируем, что по абсолютной величине коэффициенты всех трех составляющих в двух первых выражениях больше, чем в последнем, что свидетельствует об их более богатом содержании информации о цветности.

Теорема I. Координаты цветности двух дополнительных цветов равны по своей абсолютной величине, но имеют разные знаки; точки, символизирующие на цветовом графике два дополнительных цвета, располагаются симметрична по отношению к началу координат.

Возьмем два цвета, характеризуемые составляющими

R 1G 1B 1 и R 2G 2B 2 .

Если эти цвета аддитивно дополнительные, то сумма их координат равна координатам белого цвета; тогда

R 1 + R 2 = 1 (5)

G 1 + G 2 = 1 (6)

B 1 + B 2 =1 (7)

и

Y 1 + Y 2 =1 (8)

Вычитание уравнения (8) из уравнения (5) дает результат:

( R 1— Y 1 ) + ( R 2— Y 2 ) = 0

или

R 1— Y 1 = — ( R 2— Y 2 ). (9)

Вычитание уравнения (8) из уравнения (7) дает результат:

( B 1— Y 1 ) + ( B 2— Y 2 ) = 0

или

B 1— Y 1 = — ( B 2— Y 2 ). (10)

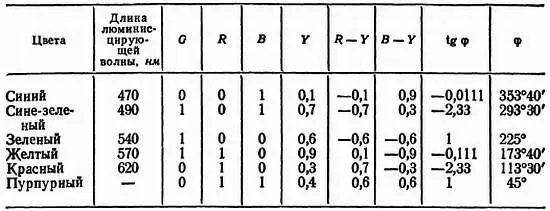
Равенства (9) и (10) определяют координаты двух точек, расположенных симметрично по отношению к началу координат точке О . Как видно из графика (рис. 21), желтый цвет служит дополнительным синему, пурпурный — зеленому и сине-зеленый — красному.

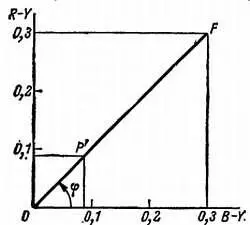
Рис. 21. График цветности с обозначением точки, соответствующей насыщенному пурпурному цвету: р( R= 0,5; G= 0; В= 0,5). Угол φ= 45° характеризует пурпурный цветовой тон. Точка р'соответствует цвету с таким же цветовым тоном ( φ= 45°), с такой же яркостью ( Y= 0,2), но с меньшей насыщенностью: р'( r = 0,286; g= 0,143; b= 0,286). Эти цвета вычитаются один из другого; для этого нужно добавить некоторое количество qбелого в более насыщенный ( q= 0,5) и разделить новые значения основных цветов на величину (1 + q/ Y);

B— Y= 0,3; b— Y= 0,086

R— Y= 0,3; r— Y= 0,086

Теорема II. Равные нулю координаты цветности характеризуют нейтральный серый цвет. Точка, символизирующая нейтральный серый, черный или белый цвета, находится у начала координат графика цветности.

Действительно,

R — Y = B — Y = 0

применяя уравнение D), выводим;

G — Y = 0

и, следовательно, получаем:

R = G = B = Y ,

а мы знаем, что цвет, состоящий из равных количеств всех трех основных цветов, по своей природе ахроматичен (закон Ньютона). Следовательно, нейтральный серый цвет полностью характеризуется одной своей яркостью.

Теорема III. Расстояние Lот символизирующей цвет точки Рдо начала координат Охарактеризует насыщенность.

Представим себе цвет со следующими составляющими: R 1, G 1 и В 1 при яркости Y 1 .

Расстояние от точки Р до начала координат О равно:

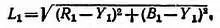
Если разбавить этот цвет путем добавления к нему некоторого количества q белого цвета, то его координаты примут следующий вид:

R 1 + q; G + q и B 1 + q при яркости Y 1 + q

Чтобы сравнить эти два цвета, имеющие все равные условия, умножим координаты на величину:

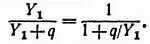
Тогда оба цвета будут иметь одинаковую яркость и будут различаться между собой только насыщенностью. Новые основные цвета будут характеризоваться следующими выражениями:

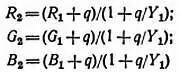
и

Y 2= Y 1.

Рассчитаем сигналы цветности:

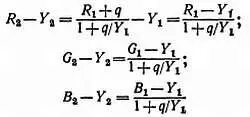
и

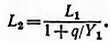
Чем больше добавляют белого, т. е. увеличивают q , или, иначе говоря, разбавляют цвет, тем при одинаковой яркости обозначающая этот цвет точка все больше приближается к началу координат.