Борис Крук - ...И мир загадочный за занавесом цифр. Цифровая связь

Итак, мы можем сказать, что скорость передачи речи в цифровом виде составляет 64000 бит/с = 64 кбит/с, а скорость передачи переведенного в цифры подвижного изображения — 104000000 бит/с = 104 Мбит/с. Текст с помощью цифр передастся обычно со скоростью 100 бит/с (это. пожалуй, самая низкая скорость передачи, исключая, разве что, передачу телеграмм — 50 бит/с); "цифровая" музыка — со скоростью 96 кбит/с; фотография в виде последовательности цифр — 16 кбит/с, а газета — 1,6 Мбит/с.

Как вы думаете, из чего состоят импульсы? Оказывается, из синусоид. Да-да, из тех самых синусоид, которые описывают колебание струны, давление звуковой волны на мембрану, а также образуют основные тоны и обертоны в речи.

Хотите убедиться в этом? Тогда взгляните на рисунок.

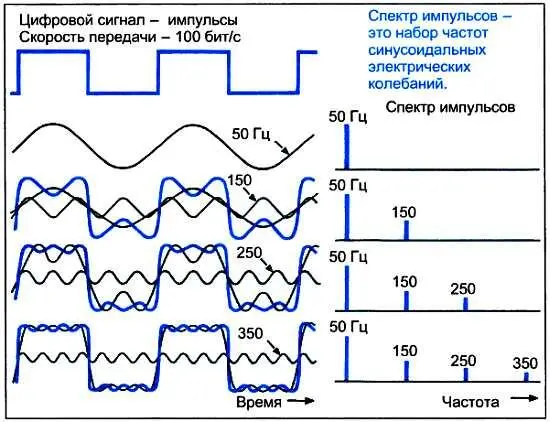
В качестве исходной синусоиды выберем такую, у которой период колебаний совпадает с периодом прямоугольных импульсов. Следующая синусоида имеет частоту колебаний в 3 раза большую, а амплитуду — в 3 раза меньшую. Сумма этих двух синусоид пока еще мало похожа на прямоугольные импульсы. Но если мы добавим к ним синусоиды с частотами колебаний в 5, 7, 9 и 11 раз большими, а с амплитудами соответственно в 5, 7, 9 и 11 раз меньшими, чем у основной синусоиды, то сумма всех этих колебаний будет не так уж и сильно отличаться от прямоугольных импульсов. Таким образом, степень "прямоугольности" импульсов определяется тем, сколько синусоид со все более и более высокими частотами колебаний мы будем суммировать.

Тот факт, что сигнал произвольной формы (а не только прямоугольные импульсы) можно "разложить" на сумму обыкновенных синусоид, впервые доказал в 20-х годах XIX в. французский математик Ж. Фурье. Такой набор синусоид получил название спектра сигнала. Каждый сигнал (отличающийся от других по форме) имеет свой сугубо индивидуальный спектр, т. е. может быть получен только из синусоид со строго определенными частотами и амплитудами.

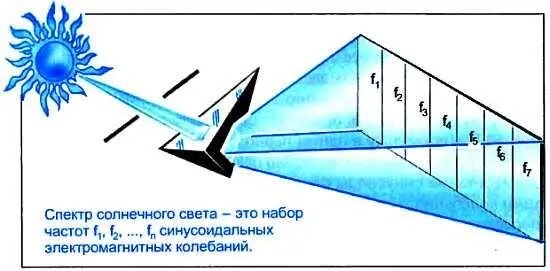
Слово "спектр" нам хорошо знакомо из других областей техники. Если, например, пропустить солнечный свет через призму, то получим цветные полосы (помните, как знакомая со школьной скамьи фраза "каждый охотник желает знать, где сидит фазан" помогала легко запомнить, на какие цвета разлагается белый свет — красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый!). Набор цветов, на которые разложили солнечный свет, и называется его спектром. Заметим, что луч какого-либо цвета — это электромагнитное колебание со строго определенной частотой. Другой цвет — другая частота колебания. Таким образом, солнечный свет представляет собой сумму простейших электромагнитных колебаний с различными частотами.

Может показаться, что представление прямоугольных импульсов в виде совокупности синусоид есть не более чем математический прием и не имеет никакого отношения к реальности. Однако это не так. Если бы вам удалось подобрать струны с частотами колебаний, кратными числам 1, 3, 5, 7…., и, расположив их рядом друг с другом, привести в движение так, чтобы амплитуды колебаний соответствующих струн соотносились как 1, 1/3, 1/5, 1/7 то вы бы увидели, что форма кривой звукового давления на мембрану микрофона (а значит, и форма тока в его цепи) была бы прямоугольной. Радиоинженерам хорошо знакомы приборы (они называются анализаторами спектров), которые позволяют выделить каждую входящую в сложный сигнал синусоиду.

Теперь займемся несложными подсчетами. Предположим, со скоростью 100 бит/с передается последовательность импульсов, соответствующая чередованию единиц и нулей: 10101010… Ее спектр будет содержать основную синусоиду с частотой колебаний 50 Гц (поскольку в одном периоде синусоиды укладываются два импульса, ее частота численно равна половине скорости передачи), а также синусоиды с утроенной, упятеренной и т. д. частотами колебаний, т. е. 150, 250, 350 Гц… В то же время для этой же последовательности, но передаваемой со скоростью 64 кбит/с, частота колебании основной синусоиды будет равна 32 кГц, а остальных синусоид — 96, 160, 224 кГц… Для скорости передачи, скажем, 104 Мбит/с картина спектра будет иная: частоты колебаний синусоид составят 52, 156, 260, 354 МГц…. Обратите внимание, они почти в 1 000 раз выше, чем во втором случае, и в 1 млн раз — чем в первом!