Юрий Ревич - Занимательная микроэлектроника

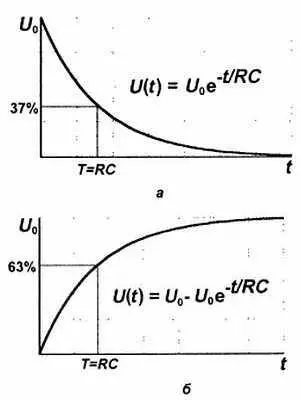
Рис. 2.9. Процессы при разряде ( а) и заряде ( б) конденсатора:

С— емкость, R— сопротивление нагрузки, t— время, e— основание натуральных алгоритмов (2,718282)

Нужно отметить два момента. Во-первых, если сопротивление резистора R на рис. 2.8 (если включить в него как сопротивление проводов и ключа, так и — при заряде — внутреннее сопротивление батареи) не равно нулю, то получается, что процессы разряда и заряда по рис. 2.9 длятся бесконечно? Да, теоретически полностью конденсатор не разрядится и не зарядится никогда, но практически это почти не имеет значения, потому что напряжение на конденсаторе становится близким к нулю или к напряжению питания очень быстро.

Во-вторых, из формул на рис. 2.9 следует очень интересный вывод: если сопротивление R равно нулю, то время процесса разряда или заряда становится бесконечно малым, а ток через нагрузку, согласно закону Ома, бесконечно большим! Обратимся снова к рис. 2.8, нечто подобное должно происходить при переключении ключа К в положение заряда емкости от батареи. Естественно, в реальной жизни ни о каких бесконечных токах речи не идет, для этого батарея должна иметь нулевое выходное сопротивление, т. е. бесконечно большую мощность (подумайте, почему эти утверждения равносильны?), а проводники должны обладать нулевым сопротивлением. Поэтому на практике процесс заряда от источника (и разряда при коротком замыкании пластин) происходит за малое, но конечное время, а ток, хоть и не бесконечно велик, но все же может достигать очень больших значений.

Значение тока в первый момент при включении конденсатора в цепь очень важно для практики. Например, под него надо рассчитывать кратковременную перегрузочную способность источника питания — иначе вы ничего не сможете включить в такой источник, потому что в первое же мгновение сработает защита, несмотря на то, что номинально мощности должно хватать. Как рассчитать этот ток? Для этого нужно представить, что конденсатор при заряде в первый момент времени ведет себя так, как будто цепь в месте его установки замкнута накоротко (это очень точное представление!). Тогда ток определится просто по закону Ома, в который подставляется сопротивление проводов и контактов (плюс, если это требуется, внутреннее сопротивление источника).

Интуитивно кажется, что должна существовать какая-то объективная характеристика цепи из конденсатора и сопротивления, которая позволяла бы описать процесс заряда-разряда во времени — независимо от напряжения на конденсаторе. Такая характеристика рассчитывается по формуле Т= R∙ C. Приведением единиц мы бы здесь занимались довольно долго, потому поверьте, что размерность произведения RC есть именно время в секундах. Эта величина называется постоянной времени RC-цепи и физически означает время, за которое напряжение на конденсаторе при разряде его через резистор (рис. 2.9, а ) снижается на величину 0,63 от начального (т. е. до величины, равной доле 1/ е от первоначального U 0, что и составляет примерно 37 %). За следующий отрезок времени, равный RС, напряжение снизится еще на столько же от оставшегося и т. п. — в полном соответствии с законом экспоненты. Аналогично при заряде конденсатора (рис. 2.9, б ), постоянная времени Т означает время, за которое напряжение увеличится до доли (1–1/ е ) до конечного значения U 0, т. е. до 63 %. Произведение RC играет важную роль при расчетах различных схем.

Есть еще одно обстоятельство, которое следует из формулы для плоского конденсатора (см. рис. 2.7). В самом деле, там нет никаких ограничений на величины S и d — даже если развести пластины очень далеко, все же какую-то емкость, хотя и небольшую, конденсатор будет иметь. То же происходит при уменьшении площади пластин. Практически это означает, что небольшую емкость между собой имеют любые два проводника, независимо от их конфигурации и размеров, хотя эти емкости могут быть и исчезающе малы.

Этот факт имеет огромное значение на высоких частотах — в радиочастотной технике нередко конденсаторы образуют прямо из дорожек на печатной плате. А емкости между параллельными проводами в обычном проводе-«лапше» или кабеле из-за их большой длины могут оказаться значительными.

Если же учесть, что проводники имеют еще и собственное сопротивление, то мы приходим к выводу, что любую пару проводов можно представить в виде «размазанной» по длине (распределенной) RС-цепи — и это действительно так, со всеми вытекающими последствиями! Например, если подать на вход пары проводников в длинном кабеле перепад напряжения (фронт прямоугольного импульса), то на выходе мы получим картину, которая ничем не отличается от рис. 2.9, б — импульс «размажется», а если он короткий, то вообще может пропасть.