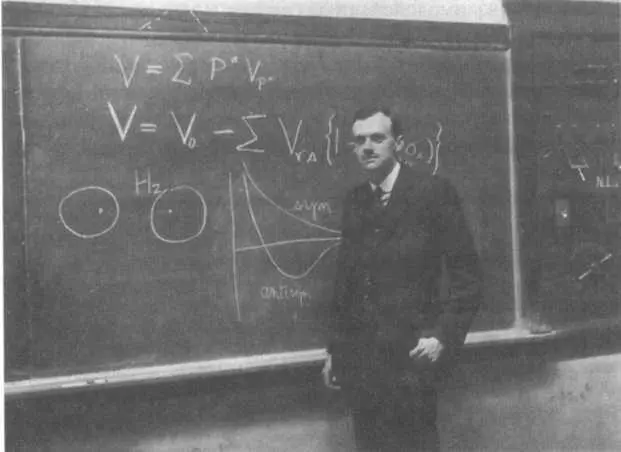Juan Carretero - Темная сторона материи. Дирак. Антивещество

Из постулатов Эйнштейна следует, что измеряемое время может замедляться в движущихся инерциальных системах; иначе говоря, оно течет быстрее, когда мы измеряем его в той же системе отсчета, в которой и находимся (в «собственной» системе). Наконец, и длина предмета зависит от системы, в которой он измеряется, поскольку определить длину означает определить одновременно края этого предмета. Эйнштейн осуществил множество «мысленных экспериментов», чтобы данный аспект стал очевидным. И если релятивистские эффекты — сокращение длины и замедление времени — незаметны в повседневном мире, для которого механика Ньютона является достаточно точной, то они играют ключевую роль в объяснении субатомных процессов.

Еще один важный принцип, следовавший из теории относительности и оказавший серьезное влияние на квантовую теорию, — принцип эквивалентности массы и энергии. В релятивистской теории масса тела зависит от системы отсчета, она увеличивается вместе со скоростью и тяготеет к бесконечности, когда скорость тела приближается к скорости света. Соотношение между массой и общей энергией тела выражается знаменитым уравнением Эйнштейна: Е = mc 2. Оно описывает эквивалентность массы и энергии и означает, что излучение или взаимодействие, то есть энергия, могут переходить в массу (в частицы), и наоборот, что частицы (масса) могут разрушаться, производя энергию. Это уравнение сыграло огромную роль

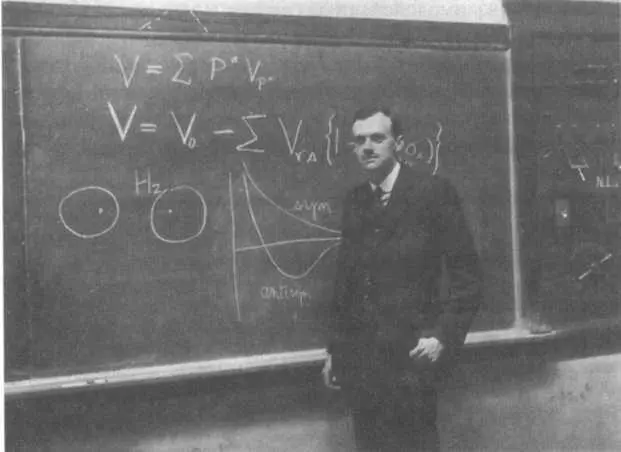
Дирак в учебной аудитории.

Поль Дирак (четвертый слева) с коллегами во время VII Сольвеевского конгресса, который был организован в 1933 году и посвящен структуре и свойствам атомного ядра. в открытии взаимодействия излучения с веществом в рамках квантовой теории. Дирак стал первым ученым, сумевшим логично соединить релятивистскую теорию с квантовой моделью. Постулирование неинерциальных систем отсчетов привело Эйнштейна к разработке общей теории относительности, он опубликовал ее в 1916 году.

Время, в которое происходит какое-либо событие, так же как и длина предмета, зависят от инерциальной системы отсчета, в которой они измеряются. В свете теории относительности эти эффекты выражаются следующими уравнениями:

Δt = γΔt 0; L = L 0/γ

где Δt 0и L 0означают измеряемые время и длину в движущейся системе отсчета, а Δt и L показатели, измеряемые в неподвижной системе. Член уравнений у, называемый «фактором Лоренца», выражается так:

γ = 1/(√(1-(v/c)2)

В обычной жизни скорость предметов (V) слишком мала по отношению к скорости света (с). В этой ситуации фактор Лоренца практически равен 1. Таким образом, нет никакой разницы между длиной или временным интервалом, измеряемыми разными наблюдателями. Принципиально иная ситуация наблюдается в субатомном мире, где скорости сопоставимы со скоростью света. Фактор у там значительно больше 1, что влечет за собой растяжение времени (Δt > Δt 0и сокращение длины (L < L 0). Данные эффекты хорошо заметны в случае мюонов. Эти элементарные частицы образуются, когда космические лучи (лучи из внешнего пространства) проникают в земную атмосферу. Как показано на схеме, мюоны появляются приблизительно на высоте 15 км от поверхности Земли. В среднем они распадаются за 2·10 -6секунд, если измерять время в их собственной системе. В механике Ньютона мюон, перемещаясь со скоростью, близкой к скорости света, мог пройти расстояние в 600-700 м до своего распада и, следовательно, никогда не мог достигнуть земной поверхности. Однако значительное количество мюонов достигало земли. Как такое возможно? Теория относительности объясняет данное явление. В инерциальной системе Земли средняя жизнь мюонов приблизительно в 20 раз дольше, чем в их собственной системе. Это означает, что мюон может преодолеть расстояние в 15 км (измеряемых в земной системе), совпадающее с толщиной атмосферы, через которую он должен пройти до своего распада на земной поверхности. Теория относительности предлагает похожее объяснение сокращения длины. В системе мюона в состоянии покоя толщина атмосферы значительно меньше, она уменьшается до 600-700 м (то самое расстояние, которое мюон проходит за свою среднюю жизнь, измеряемую в его собственной системе).