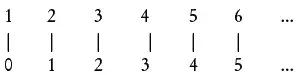
Набор остался той же мощности, несмотря на то, что мы из него кое-что убрали. На самом деле из набора целых чисел мы можем убрать бесконечное количество элементов — можем исключить, например, нечетные числа — мощность множества останется неизменной. Все по-прежнему имеют места, и каждое место занято.
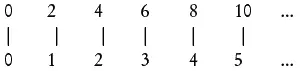
Это есть определение бесконечного: это нечто, что может оставаться той же мощности, даже если вы из него что-то вычтете.
Четные числа, нечетные числа, целые числа — все эти множества имеют одинаковую мощность, размер, которую Кантор обозначил как 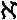 0 (алеф-ноль, названный так по первой букве еврейского алфавита). Поскольку эти наборы имеют ту же мощность, что и множество натуральных чисел, любое множество мощности
0 (алеф-ноль, названный так по первой букве еврейского алфавита). Поскольку эти наборы имеют ту же мощность, что и множество натуральных чисел, любое множество мощности 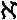 0называется счетным. (Конечно, на самом деле вы не можете их пересчитать, если не располагаете бесконечным временем.) Даже множество рациональных чисел — множество чисел, которые могут быть записаны как a / b для целых чисел a и b, — является счетным. Ловко отведя рациональным числам подобающие места, Кантор показал, что рациональные можно «рассадить» по стульям с натуральными номерами, то есть что они образуют множество размера
0называется счетным. (Конечно, на самом деле вы не можете их пересчитать, если не располагаете бесконечным временем.) Даже множество рациональных чисел — множество чисел, которые могут быть записаны как a / b для целых чисел a и b, — является счетным. Ловко отведя рациональным числам подобающие места, Кантор показал, что рациональные можно «рассадить» по стульям с натуральными номерами, то есть что они образуют множество размера 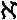 0(см. Приложение D).
0(см. Приложение D).
Однако, как было известно Пифагору, рациональные числа вовсе не заполняют все под солнцем. Рациональные и иррациональные числа в совокупности составляют так называемые вещественные числа. Кантор открыл, что множество вещественных чисел много больше множества рациональных чисел. Его доказательство было очень простым.
Представьте себе, что у вас имеется идеальный план «рассадки» вещественных чисел: каждое вещественное число имеет место, и каждое место занято. Это означает, что мы можем сделать список мест с указанием номера места одновременно с тем вещественным числом, которое на нем сидит. Например, наш список мог бы выглядеть примерно так:
Место . . . . . . . . . . Вещественное число
1 . . . . . . . . . . . . . . 3125123…
2 . . . . . . . . . . . . . . 7843133…
3 . . . . . . . . . . . . . . 9999999…
4 . . . . . . . . . . . . . . 6261000…
5 . . . . . . . . . . . . . . 3671123…
и т.д. . . . . . . . . . . .и т.д.
Уловка удалась, когда Кантор создал вещественное число, которого не было в списке.
Посмотрите на первую цифру первого числа в списке. В нашем примере это 3. Если бы наше новое число было равно первому числу в списке, его первой цифрой тоже было бы 3, но мы с легкостью можем воспрепятствовать этому. Давайте просто скажем, что наше новое число начинается с цифры 2. Поскольку первое число в списке начинается с 3, а новое число — с 2, мы знаем, что эти числа различны. (В строгом смысле слова это не так. Число 3,00000… равно числу 2,99999…, поскольку существует два способа записи многих рациональных чисел. Однако это мелочь, которую легко преодолеть. Для ясности мы проигнорируем это исключение.)
Теперь перейдем ко второму вещественному числу. Как мы можем быть уверенными в том, что наше новое число отличается от второго числа из списка? Что ж, мы уже определили первую цифру нашего нового числа, так что не можем повторить в точности ту же уловку, но можем сделать кое-что не хуже. Второе число нашего списка имеет вторую цифру 8. Если наше новое число имеет вторую цифру 7, мы можем убедиться, что наше новое число не совпадает со вторым числом из списка, поскольку их вторые цифры отличаются друг от друга. Значит, они не одинаковы. Мы продолжаем делать то же самое, двигаясь по списку: рассматриваем третью цифру третьего числа и меняем ее, рассматриваем четвертую цифру четвертого числа и меняем ее — и так далее.


Это дает новое число 27800…, которое отличается от первого числа (их первые цифры не совпадают), от второго числа (их вторые цифры не совпадают), от третьего, четвертого, от пятого и т.д.
Перемещаясь подобным образом по диагонали, мы создаем новое число. Этот процесс обеспечивает отличие нового числа от всех чисел в списке. Оно отлично от всех чисел в списке, оно не может входить в список, но мы уже предположили, что наш список содержит все вещественные числа. В конце концов, это был полный список рассаженных чисел. Имеет место противоречие. Безупречный список «рассадки» существовать не может.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

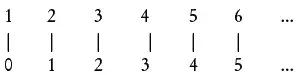
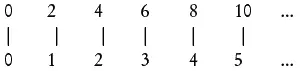
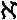 0 (алеф-ноль, названный так по первой букве еврейского алфавита). Поскольку эти наборы имеют ту же мощность, что и множество натуральных чисел, любое множество мощности
0 (алеф-ноль, названный так по первой букве еврейского алфавита). Поскольку эти наборы имеют ту же мощность, что и множество натуральных чисел, любое множество мощности 










