Давид Ласерна - Эйнштейн. Теория относительности. Пространство – это вопрос времени.

Карл Фридрих Гаусс (1777-1855) по масштабу своего мышления может сравниться разве что с Ньютоном или Архимедом. Некоторые из самых значительных его открытий, такие как неевклидова геометрия и алгебра комплексных чисел, не были опубликованы, чтобы избежать научных споров. Гаусс мог себе это позволить: напечатанной части его работ было достаточно, чтобы произвести переворот в математике. Риман обобщил идеи Гаусса в дифференциальной геометрии. В 1854 году он прочитал лекцию на эту тему, завершив выступление словами: «Это приводит нас в сферу другой науки, физики, куда сегодня мы не можем углубиться». Риман остановился на границе, которую осмелился пересечь только Альберт Эйнштейн, родившийся четверть века спустя. Однако познать тайну строения космоса ему помогли разработанные Риманом математические инструменты.

До начала XIX века и публикации работы Гаусса «Общие исследования о кривых поверхностях» двумерные пространства рассматривались с трехмерной перспективы, словно со стороны. Заслуга Гаусса состоит в том, что он погрузился в саму поверхность, сталкиваясь, по мере своего продвижения, с различными новыми задачами. Это воображаемое путешествие стало первым шагом в изучении внутренней геометрии поверхностей, которая получила мощный толчок в развитии благодаря одному из учеников Гаусса, Бернхарду Риману (1826-1866).

Когда речь идет о плоскости, кажется разумным экстраполировать свойства небольшого участка на другие, близкие ему. Однообразие плоскости подразумевает, что все ее участки идентичны. Однако в более сложной среде каждая неровность становится новой точкой отсчета. Мы различаем возвышения и углубления, и особенности одного участка плоскости нельзя приписать другому ее участку. Следовательно, чтобы изобразить внутреннюю структуру поверхности, мы должны составить карту всей ее площади.

Для того чтобы это сделать, Гаусс обратил внимание на то, что произойдет, если мы возьмем любую точку на поверхности и немного продвинемся от нее в случайном направлении. Если мы находимся на плоской поверхности, такой, например, как пол в доме, то в каком бы направлении мы ни двигались, пройденный путь будет равен расстоянию до точки. Но на изогнутой поверхности все оказывается сложнее. Двинувшись направо, мы, возможно, спустимся вниз, а повернув налево, можем обнаружить крутой подъем.

В качестве примера рассмотрим положение двух людей на рисунке со следующей страницы. Оба двигаются от точки А к точке В, расположенной неподалеку. Первый человек идет по прямой линии на плоском участке, а второй движется в углублении. Чтобы дойти от А до В, второй человек должен пройти больше, чем первый, из-за геометрической кривизны участка (рисунок 10). И для каждого из них расстояние от А до В будет разным.

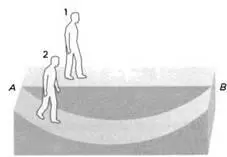
РИС. 10

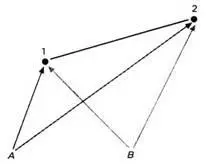
РИС. 11

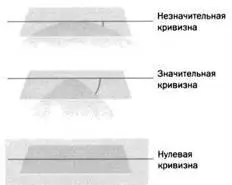
РИС. 12

Гаусс ввел новую математическую функцию, метрику (она обозначается буквой g), которая показывает расстояние до точки поверхности в зависимости от того, в каком направлении мы движемся. Как вы уже понимаете, на неровной поверхности эта информация от точки к точке меняется.

Метрику можно считать руководством по устройству поверхности, поскольку она содержит все интересующие нас данные. Когда рассматриваешь пространство из более высокого измерения, его неровности становятся заметны невооруженным взглядом, а метрическая функция позволяет нам оценить их, находясь непосредственно на поверхности.

Геометрические свойства поверхности должны быть независимы от системы координат, выбранной для ее описания, – так же, как в новостях, на какой бы язык мы их ни перевели, речь должна идти об одном и том же. Расстояние между двумя точками – это информация, которая не меняется с «переводом», то есть с изменением координат. Точки 1 и 2 находятся на разных расстояниях от точек А и В, но расстояние между ними самими не меняется, то есть, на языке алгебры, расстояние является инвариантом (рисунок 11). С помощью метрической функции возможно определить расстояние между любыми двумя точками на поверхности. Также она позволяет построить другие инварианты, например кривизну, то есть величину, выражающую, насколько отклоняется поверхность от евклидовой плоскости (рисунок 12).