Законы Максвелла не были похожи на законы Ньютона: при преобразовании Галилея они изменялись. В любой инерциальной системе отсчета можно выразить силу как произведение массы на ускорение без необходимости добавлять новые понятия из-за изменившихся координат. Но уравнения Максвелла претерпевают метаморфозы, сравнимые с превращением доктора Джекила в мистера Хайда[2 «Странная история доктора Джекила и мистера Хайда» – повесть шотландского писателя Роберта Стивенсона о том, как в одном человеке уживаются две совершенно не похожие друг на друга личности. – Примеч. ред.]. В неподвижной системе отсчета они выглядят лаконично и элегантно, но при переводе с помощью формулы [2] в движущуюся систему, например корабль Доминика, появляются различные новые элементы, значительно усложняющие исходные уравнения. Эти элементы соответствуют физическим явлениям, которые никто не видел. Например, линии магнитного поля вокруг магнита в состоянии покоя непрерывны, но в движении становятся разорванными. Оказывается, что уравнения Максвелла не были слепы к постоянной скорости и позволяли обнаружить равномерное передвижение.
Любопытно, что Максвелл вывел свои элегантные формулы, основываясь на явлениях, которые происходят на поверхности Земли – и все согласятся, что эта система отсчета является движущейся. Возможно ли, что в сравнении с другими системами отсчета планета Земля имела свои преимущества? Этот вопрос ставил физиков на край геоцентрической пропасти. Неужели Библия говорит правду и небесные светила движутся вокруг нашей планеты? Действительно ли только на Земле и больше ни в какой движущейся системе отсчета уравнения Максвелла проявляют всю свою силу и простоту?
Поскольку уравнения Максвелла равно просты в обеих системах отсчета, G и Д электромагнитные эксперименты тоже не годятся для того, чтобы установить, двигается наблюдатель с постоянной скоростью или находится на причале в состоянии покоя.
Для того чтобы разрешить это противоречие, потребовалось поправить формулы преобразования Галилея, несмотря на всю их логичность. В 1904 году нидерландский ученый Хендрик Лоренц (1853-1928) предложил новый набор уравнений для перевода координат из одной системы отсчета в другую, при условии, что системы отличаются параметром постоянной скорости одной из них. Научное сообщество отметило событие, дав уравнениям имя изобретателя – так на свет появились преобразования Лоренца.
Преобразования Лоренца
Выглядят они следующим образом:
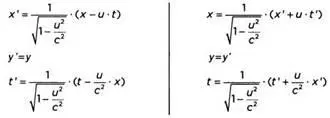
Достаточно внимательно посмотреть на формулу, связывающую t' с t и х, и вы заметите некую странность. Определенному моменту времени в покоящейся системе отсчета (t) соответствует множество различных значений t' – в зависимости отточки пространства, в которой мы находимся (х). Одновременные события, происходящие в двух разных точках причала, будут разнесены во времени, если наблюдать их из трюма корабля. Кроме того, оказалось, что при скорости меньшей, чем скорость света (когда u²/с² и u/с² практически равны нулю), уравнения сводятся к преобразованиям Галилея. Попробуем представить себе масштаб коррекции.
Рассчитаем величину u²/с² в случае идущего человека (шагает он со скоростью примерно 5 км/час) и в случае летящей пули (предположим, ее скорость равна 1000 м/сек). Получаем 2.1 • 10-17 и 1,1 • 10-11 соответственно. Преобразования приятны глазу физика, и между переменными есть определенная симметрия. Если х' зависит от х и t, t' также зависит от них. В случае Галилея время t’ не зависело отточки пространства х'. Это преобразование вызвало у математиков ощущение дежа вю: оно напоминало уравнения вращения объектов в пространстве. Аналогия привела к тому, что был сконструирован такой пространственно-временной континуум, в котором преобразования Лоренца соответствуют вращению объектов в пространстве с четырьмя измерениями.

Отметим их большой плюс: в применении к уравнениям Максвелла преобразования Лоренца позволяют сохранить их восхитительную лаконичность. А при скорости движения намного меньшей, чем скорость света, они принимают вид преобразований Галилея. Поскольку скорости, с которыми мы обычно передвигаемся, очень малы по сравнению со скоростью света, неудивительно, что наш здравый смысл не сразу привел нас к уравнениям Лоренца и в течение нескольких веков удовлетворялся примерными расчетами Галилея. Необходимая коррекция так мала, что была обнаружена не в лабораториях, а с помощью теоретических рассуждений.
Читать дальше

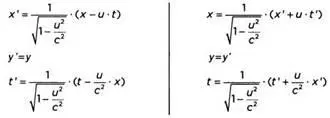





![Николь Валентайн - Теория относительности с точки зрения путешественника во времени [litres]](/books/385217/nikol-valentajn-teoriya-otnositelnosti-s-tochki-zr-thumb.webp)
![Коллектив авторов - Происхождение Вселенной. Как с помощью теории относительности Эйнштейна можно проникнуть в прошлое, понять настоящее и предвидеть будущее Вселенной [litres]](/books/414554/kollektiv-avtorov-proishozhdenie-vselennoj-kak-s-p-thumb.webp)





