Roger Orrit - Природа описывается формулами. Галилей. Научный метод.

Галилей предвидел, что в результате эксперимента, подобного тому, что проделали американские космонавты с молотком и пером, оба предмета упадут на поверхность одновременно. Его опыты с наклонной плоскостью во время изучения свободного падения показали, что скорость, развиваемая шарами, зависит только от высоты плоскости, а не от их веса. Таким образом, ученый обосновал свои заключения эмпирическими данными, но не стал объяснять причины этого явления (он систематически воздерживался от безосновательных измышлений), поскольку недостаточно разработал математические методы, способные доказать независимость массы от скорости падения тел.

Исходя из принципов Ньютона возможно математически показать, что скорость, приобретаемая телом во время свободного падения, зависит исключительно от силы притяжения, а не от массы. К тому же, зная радиус и массу планет и спутников, мы можем рассчитать значение ускорения свободного падения на их поверхности.

По Ньютону, между любыми массами возникает притяжение. При помощи своего закона всемирного тяготения он рассчитал эту силу и установил, что она прямо пропорциональна массе двух тел (m 1и m 2) и обратно пропорциональна квадрату расстояния между этими телами (d). В соответствии с этим, закон всемирного тяготения выглядит так:

F=G·(m 1-m 2)/d²

где G — гравитационная постоянная, равная 6,67·10 -11Н·м²/кг².

Вместо взаимодействия двух масс представим себе единое тело, которое ни с чем не взаимодействует. В этом случае, хотя оно и не действует непосредственно ни на какое другое тело, предполагается, что вокруг него создается некое поле, так, что как только другое тело приблизится к этому полю, то сразу же попадет под его влияние. Это гравитационное поле можно изобразить в виде линий, направленных в центр притяжения, то есть к телу (рис. 1).

РИС. 1

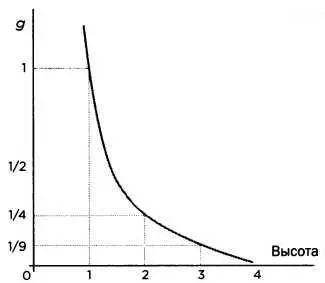
РИС. 2

Значение гравитационного поля можно рассчитать по следующей формуле:

g=G·m 1/d² [1]

По этому уравнению мы видим, какое влияние будет оказано на любую массу m 2,которая находится на некотором расстоянии от первого тела. Для этого надо будет просто вычислить F=m 2g.

Изучив уравнение гравитационного поля, мы увидим, что при увеличении расстояния от центра массы, создающей это поле, уменьшается его интенсивность. Уменьшение силы тяготения в зависимости от высоты можно изобразить в виде графика (рис. 2).

Если в формулу [1] мы подставим массу Земли, а в качестве расстояния возьмем средний радиус Земли:

— масса Земли: М 3= 5,9736·10 24кг;

— радиус Земли: d = 6371 км = 6,371·10 6м; то получим следующий результат:

g=G·M 2/d 2= 6,67·10 -11Η·м 2/кг 2·(5,9736·10 24кг)/(6,371-10 6) 2м 2=9,81 м/с 2.

Таким образом, на уровне моря все тела имеют одинаковое ускорение (9,81 м/с 2).

С помощью этой же формулы можно вычислить интенсивность гравитационного поля на вершине горы или показать, как уменьшается его значение в зависимости от высоты. Эти расчеты можно произвести и применительно к Луне:

— масса Луны: М л= 7,349·10 22кг;

— радиус Луны: 1,738 106 м;

g=G·М л/d 2= 6,67·10 -11Η·м 2/кг 2·7,349·10 22кг/(1,738- 10 6) 2м 2=1,62 м/с 2.

Так мы можем получить значение ускорения на Земле и на Луне. Зная радиус и массу любой планеты или спутника, можно вычислить ускорение свободного падения. Чем крупнее и плотнее планета, тем больше будет значение, определяющее ускорение, с которым будут падать на ней тела. Гравитационное поле также определяет, какую скорость должно развить тело, чтобы освободиться от его влияния и удалиться от планеты или спутника.

По законам кинематики положение и скорость тел при свободном падении вычисляются исходя из их массы. Рассчитывая скорость тела во время свободного падения при помощи понятий кинетической энергии (E c, связанной со скоростью) и потенциальной энергии (E p, связанной с весом), можно еще раз убедиться, что эта скорость зависит не от массы тела, а только от высоты, на которой оно находится:

E c= ½mv 2

E p= m·g·h.

Когда мы держим шар на определенной высоте от поверхности, он обладает потенциальной энергией, которая при его падении переходит в кинетическую. Таким образом, для того чтобы узнать, какова будет скорость тела в момент, когда оно коснется земли (то есть когда вся его потенциальная энергия перейдет в кинетическую), нужно использовать формулу: