Борис Штерн - Прорыв за край мира

Где-то году в 1982-м в столовой ФИАН произошел разговор, который хорошо запомнился Игорю Ткачёву. Рассказ об этом разговоре заслуживает того, чтобы передать его полностью.

20.1. Игорь Ткачёв иллюстрирует варианты туннельного перехода инфлатона — как это предполагалось в работе Гута (вверху) и как это должно происходить на самом деле (внизу). Снимок Б. Штерна

Игорь Ткачёв о давнем разговоре с Андреем Линде

В то время, когда работа Гута по инфляции была у всех на слуху, Андрей рассказал про некоторые свои соображения по этому поводу. Это было в фиановской столовой. Как сейчас помню, ели борщ.

В сценарии Гута инфляция заканчивается, когда поле туннелирует через потенциальный барьер. Он считал, что туннелирование происходит сразу из локального минимума в основной, как на верхнем рисунке. Для оценки вероятности он использовал так называемое тонкостенное приближение. В его сценарии образовывалось много пузырей новой фазы, которые сталкивались и объединялись в горячую однородную вселенную.

Андрей сказал, что это большой вопрос, куда туннелирует поле. А если потенциал устроен так, что второго минимума нет и кривая уходит вообще вниз? Что тогда — туннельный переход произойдет в минус бесконечность? Да нет, конечно! То, куда оно перейдет, надо считать, и тонкостенное приближение здесь не годится. Потенциал после туннельного перехода не может стать выше из-за закона сохранения энергии. Ниже может, но не сильно ниже — вероятность этого очень мала: под барьером наберется больший отрицательный интеграл действия, который идет в экспоненту, когда считаешь вероятность.

Андрей честно посчитал, куда с наибольшей вероятностью попадает поле после туннельного перехода, причем считать пришлось на компьютере — это не так просто. Оказалось, поле туннелирует немного ниже минимума на склон, как на нижнем рисунке. И здесь, на склоне, его значение велико — не намного ниже, чем в локальном минимуме. Андрей посчитал, что происходит после этого — тут считать даже легче. Оказалось, что инфляция отнюдь не заканчивается. Поле продолжает раздувать пространство и успевает раздуть его на много порядков, пока не «сползет» вниз по склону.

Из этого следовали важнейшие вещи: сценарий Гута неверен в своем конце — пузыри новой фазы, протуннелировавшие через барьер, не успевают объединиться, перемешаться и разогреться, дав однородную горячую вселенную, — они разносятся на огромные расстояния. И второе следствие: не нужно изобретать хитрые потенциалы с барьером. Инфляция может работать и без них. Это очень серьезные следствия, и Андрей, еще не очень доверяя своим результатам, стремился обсудить их с возможно большим числом коллег, заручившись поддержкой и уверенностью перед публикацией статьи.

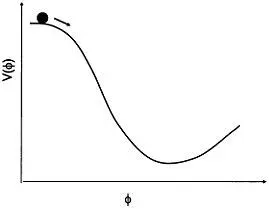
Рис. 20.2. Потенциал инфлатона в модели «новой инфляции»

Итак, потенциальный барьер был призван задержать скалярное поле в локальном минимуме, чтобы оно успело раздуть вселенную прежде, чем «упадет» в основное состояние. Но, оказывается, поле и без барьера может «застрять» вблизи своего первоначального значения. Для этого нужно, чтобы расширение было быстрым, а потенциал поля пологим. На языке хорошо знакомых явлений быстрое расширение играет роль вязкого трения, а наклон потенциала V{(p) аналогичен наклону поверхности, по которой катится шарик. Есть разные возможности сконструировать скалярное поле. Вариант, предложенный взамен сценария Гута Андреем Линде и на три месяца позже Андреасом Альбрехтом и Полом Стейнхардтом, — потенциал с плоской вершиной при нулевом поле и минимумом в стороне, как изображено на рис. 20.2.

Вход в стадию инфляции, как и в сценарии Гута, — термодинамический: горячая протовселенная расширяется и адиабатически охлаждается. Если в начале поле находится в термодинамическом равновесии при высокой температуре, оно должно «сесть» в нуль. Это довольно общее свойство систем — находиться при высокой температуре в наиболее симметричном состоянии (на самом деле изображенный потенциал похож на донышко бутылки в комплексных координатах, и нуль оказывается центром симметрии). При расширении зародыша вселенной опять происходит переохлаждение, и инфляция стартует точно так же, как изложено выше. И точно так же вселенная успевает раздуться на десятки порядков величины, пока поле, преодолевая вязкое трение, катится вниз с «пологой горки».