После остановки двигателя ракета продолжает полет за счет накопленной ранее скорости, как снаряд, вылетевший из ствола артиллерийского орудия. Правда, такую пушку в данном случае надо было бы поместить на высоте 40 километров. Летя таким образом, ракета забирается еще выше и достигает максимальной высоты — примерно 100 километров.
Но и 100 километров — это совсем не предел, достигнутый современной реактивной техникой, как не предел и достигнутая скорость полета в 1,5 километра в секунду. Использование идей Циолковского позволило добиться уже значительно больших успехов в том замечательном штурме мирового пространства, который ведет реактивная техника.
Какие же это идеи?
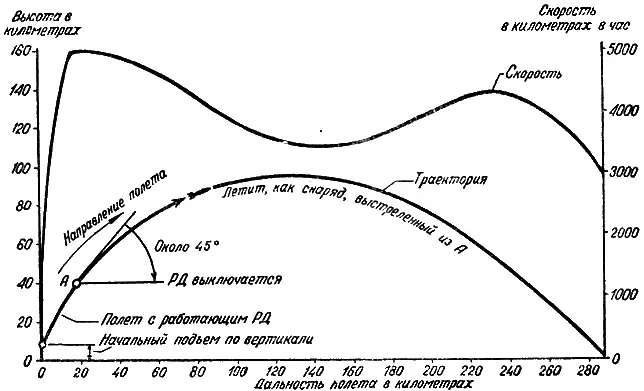
Траектория и скорость полета ракеты.
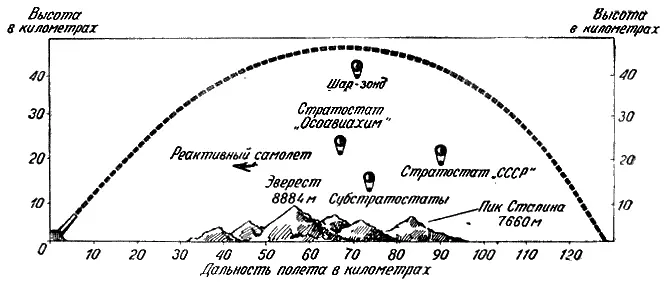
Траектория артиллерийского снаряда.
Глава 7
«ТАЮЩИЕ» СНАРЯДЫ И «ТАЮЩИЕ» ПОЕЗДА
Раз известно, какую скорость нужно сообщить межпланетному кораблю, и найден двигатель для него, то не должно быть ничего трудного в том, чтобы рассчитать межпланетный корабль — определить нужный запас топлива, общий вес корабля, траекторию полета. Однако первые же попытки Циолковского решить сначала более простые задачи — например, определить, как далеко залетит какая-нибудь ракета или как высоко она поднимется, — натолкнулись на несколько неожиданное препятствие. Оказалось, что подобных задач до Циолковского еще никто не решал. Выяснилось также, что это не такие уж простые задачи.
Известно, что законы движения различных тел изучает наука о движении — механика, созданная Ньютоном. Естественно, что в поисках нужного ему решения Циолковский обратился за помощью к механике. Однако в то время эта наука оказалась бессильной помочь Циолковскому.
До Циолковского механика имела дело всегда с телом определенной массы. И это всех устраивало, ибо на практике только такие случаи и встречались. Трудно было себе представить, например, задачу о падении какого-нибудь камня, который бы в полете «худел», теряя массу.
Но перед Циолковским стояли, увы, именно такие задачи. Масса ракеты в полете сильно изменяется, так как часть массы ей приходится отбрасывать в виде продуктов сгорания топлива. Поэтому ракета, пока работает ее двигатель, не похожа на обычные снаряды. Это какой-то особый, быстро «тающий» в полете снаряд. Вспомните, например, ракету, описанную в предыдущей главе. За одну минуту полета с работающим двигателем ее вес уменьшается с 13 до 4 тонн. Поистине катастрофическое «похудание»…
Чтобы научиться рассчитывать полет ракет, нужно было сначала разработать новую главу механики — механику тел переменной массы. Без этого нельзя было создать и науку о движении ракет — ракетодинамику.
Честь решения этих задач принадлежит Циолковскому. И в этом — одна из наибольших его заслуг перед человечеством, перед наукой. Разработанная Циолковским механика тел переменной массы позволяет решать множество важных технических задач; она лежит и в основе теории межпланетного полета.
Интересно, что практически одновременно с Циолковским и независимо от него разработкой механики тел переменной массы занимался крупный русский ученый — профессор И. В. Мещерский, которому принадлежит решение ряда важных проблем в этой области.
И в наши дни ведущая роль в разработке вопросов ракетодинамики принадлежит советским учёным, ученикам Циолковского и Мещерского.
Чтобы изучить законы движения ракет, Циолковский рассмотрел простейший случай полета ракеты — полет ее в таком пространстве, в котором нет сопротивления воздуха и отсутствует сила тяжести. Циолковский назвал это условное пространство свободным. В таких примерно условиях будет находиться межпланетный корабль при полете в межзвездном мировом пространстве — воздуха там нет, а силой тяжести в первом приближении можно пренебречь, если корабль не находится непосредственно вблизи тяжелых небесных тел.
Главная задача, которая стояла перед Циолковским, заключалась в том, чтобы научиться определять конечную скорость ракеты, то есть ту скорость, которую ракета приобретает, когда ее двигатель останавливается из-за выработки всего топлива.
Решение этой задачи было получено впервые Циолковским и опубликовано им в 1903 году. Полученная Циолковским формула, позволяющая определить конечную скорость ракеты, имеет важнейшее значение в теории ракет и, значит, в теории межпланетного полета. Во всем мире эту формулу, так называемую формулу ракеты, знают как закон Циолковского, как формулу Циолковского. [20] См. приложение.
Читать дальше














