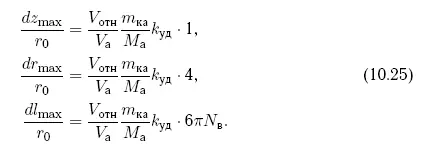Борис Шустов - Астероидно-кометная опасность - вчера, сегодня, завтра

В разделе 10.3 были получены выражения, дающие изменения координат астероида по бинормали z, радиус-вектору r и вдоль орбиты l, возникающие при появлении импульсов скорости dV S, dV T, dV W, приложенных по осям орбитальной системы координат S, T, W. Изменения координат отнесены к гелиоцентрическому радиус-вектору астероида r 0и в сводном виде представлены в табл. 10.4.

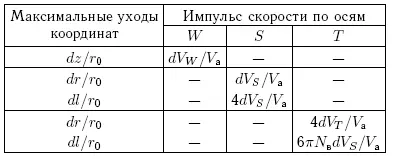
Почти все изменения координат — периодические, за исключением ухода dl/r 0вдоль орбиты астероида при условии, что приращение скорости произведено по оси Т. В этом случае изменение координаты dl/r 0имеет вековой характер и линейно нарастает с ростом числа витков орбиты астероида N в.

Все приращения скорости, создаваемые по осям S, T, W, отнесены к гелиоцентрической скорости астероида V а.

Положим, что удар по астероиду производится по осям S, T, W. Тогда, подставив в выражения, описывающие приращения относительных координат, формулы, соответствующие приращениям скорости астероида, можно получить удобные выражения для оценок итоговых максимальных изменений относительных координат, возникающих после удара:

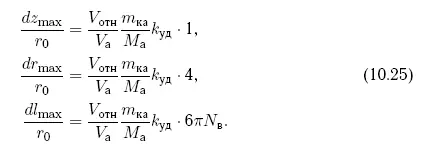
Здесь максимальные значения периодических изменений координат даны в смысле, рассмотренном в разделе 10.3. Максимальное изменение координаты dz max/r 0дается для удара, направленного по оси W. Максимальные изменения координат dr max/r 0и dl max/r 0приведены лишь для случая удара, направленного по оси T, как наиболее эффективные. При этом для координаты dl max/r 0указано значение на момент времени, соответствующий завершению витка орбиты после удара.

Рассмотрим численный пример, предполагая коррекцию орбиты астероида Апофис, выполняемую ударом космического аппарата в период до 2029 г. Масса Апофиса оценивается величиной M а ∼ 5, 0 10 10кг, а его гелиоцентрическую скорость можно принять равной V а ∼ 30 км/с. Тогда, взяв среднее значение коэффициента k уд= 3 и предполагая, что КА массой m ка= 10 3кг ударяет астероид с относительной скоростью V отн∼ 10 км/c вдоль оси T, можно получить оценку максимального изменения координат астероида по радиус-вектору, равную dr/r 0 ∼ 2 10 -8. Полагая r 0 ∼ 1,5 10 8км, нетрудно видеть, что максимальное смещение астероида составит ∼ 3 км. Следовательно, оказывается, что удар космического аппарата с разумной массой по астероиду в принципе может вывести Апофис из зоны резонансного возврата и устранить опасность встречи Апофиса с Землей в 2036 г.

Так как смещение по радиус-вектору — периодическое, то для получения максимального увода астероида необходимо выполнять удар по астероиду с упреждением относительно момента сближения Апофиса с Землей. В разделе 10.3 показано, что упреждение должно составлять примерно половину витка орбиты астероида. Отсюда следует, что выбор момента старта КА-ударника с Земли для перелета к Апофису должен быть подчинен этому условию. Поэтому обычные методики оптимизации выбора времени старта для получения максимальной массы доставляемой полезной нагрузки в данном случае могут быть неприменимы. Как следствие, масса КА может не достигать максимальных значений, возможных для выбранного носителя.

Дальнейшие, более точные оценки эффективности кинетического воздействия, по-видимому, можно будет получить только при корректном расчете тех или иных конкретных геометрических схем встречи ударного аппарата с астероидом. Однако с самого начала следует иметь в виду, что точность расчетов окончательного эффекта будет низкой вследствие побочных эффектов, сопровождающих удар.

Следовательно, применение кинетического способа увода в обстоятельствах, требующих точного выполнения расчетной коррекции траектории, по-видимому, невозможно. К таким обстоятельствам, прежде всего, нужно отнести случай близкого пролета астероида Апофис мимо Земли в 2029 г. Возможно, кинетический способ и может использоваться как начальная грубая коррекция орбиты угрожающего тела, однако по своей природе он потребует точной доводочной коррекции движения астероида какими-то другими средствами. Одно из таких средств будет рассмотрено в следующем подразделе.

В начале настоящего раздела упоминались способы воздействия на астероид путем направленного выброса вещества астероида в космос, а также за счет создания на пути угрожающего тела облака частиц или небольших объектов для торможения. Нетрудно применить к этим способам все сказанное выше для случая кинетического ударного воздействия.