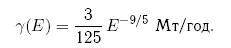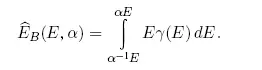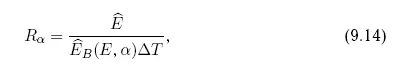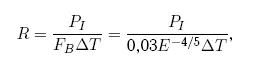Борис Шустов - Астероидно-кометная опасность - вчера, сегодня, завтра

ƒ B= 0,03E -4/5год -1, (9.12)

где энергия E исчисляется в мегатоннах.

Формула (9.12) выражает зависимость, очень близкую к эмпирическому распределению, найденному Е. Шумейкером главным образом на основании подсчета числа лунных кратеров [Shoemaker, 1983]. Заметим, что частоту падения тел на Землю при условии ее малости (именно с такими событиями приходится иметь дело) можно рассматривать как годичную вероятность событий.

На рис. 9.9 представлена частота столкновения Земли с космическими телами как функция энергии. Учитываются тела с энергией, большей или равной заданной величине E. Кривая линия — эмпирическое распределение, основанное преимущественно на результатах Шумейкера [Chapman and Morrison, 1994]. Прямая линия — аппроксимация, определяемая формулой (9.11). Для сравнения штриховой линией показана частота столкновений по Туринской шкале.

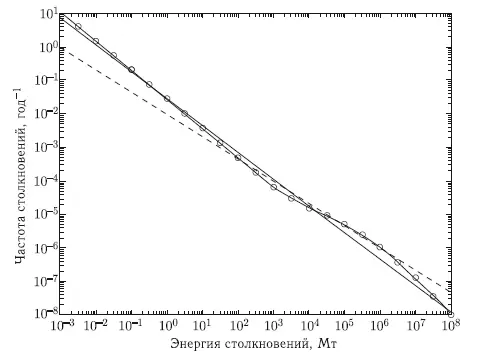
Рис. 9.9. Частота столкновения Земли с космическими телами как функция энергии [Chesley et al., 2002]

Математически величина ƒ Bпредставляет собой определенный интеграл:

где γ(E) — частота столкновения Земли с телами, обладающими энергией E. Дифференцируя интеграл (9.13) по нижнему пределу и используя формулу (9.12), находим выражение для этой частоты в виде

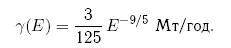
Найдем теперь ожидаемый поток энергии Ê B(E, α), приносимой на Землю в течение года падающими на нее телами в некотором диапазоне энергии от α -1E до αE:

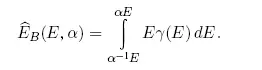
Теперь имеется возможность сравнить ожидаемую энергию столкновения Ê для рассматриваемого события с общей энергией, приносимой на Землю телами в некотором диапазоне энергии от α -1E до αE за время, оставшееся до столкновения. Последняя величина, очевидно, равна

Ê B(E, α)ΔT,

где ΔT — время до столкновения, выраженное в годах.

Искомое отношение R α, равное

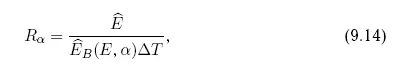
можно квалифицировать как ожидаемую энергию столкновения, взвешенную по отношению к потоку энергии, приносимой телами подобного же размера за оставшееся до столкновения время.

Можно показать, что, выбирая α равным 1,865, выражение (9.14) можно свести к следующему:

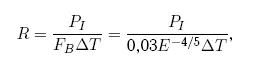
которое в Палермской шкале получило наименование «нормализованного риска». Другими словами, нормализованный риск — это вероятность столкновения тела с Землей, взвешенная по отношению к вероятности столкновения с Землей тел такой же или большей энергии за время, оставшееся до предполагаемого столкновения. Десятичный логарифм этой величины P определяет Палермскую техническую шкалу для оценки угрозы столкновения тел с Землей:

P = lg R. (9.15)

Все вышесказанное применимо равным образом и тогда, когда астероид или комета имеют на рассматриваемом интервале времени серию сближений с Землей. В этом случае вычисляется совокупный нормализованный риск, который сопоставляется с фоновым риском, исчисляемым за время до конца рассматриваемых событий.

Исходя из определения Палермской шкалы, можно отметить, что события, получающие оценку ноль, представляют такую же угрозу, которую создает естественный фон тел, способных сближаться с Землей, такой же или большей энергии. Значение шкалы –2 соответствует событию, представляющему в сто раз меньшую опасность по сравнению с естественным фоном, а оценка +3 означает событие в тысячу раз более опасное по сравнению с вероятными столкновениями Земли со случайными телами такой же энергии за время, остающееся до события.

Как связаны друг с другом Туринская и Палермская шкалы? Это разные шкалы. Не существует правила перехода от одной шкалы к другой, хотя бы уже потому, что Палермская шкала непрерывная, а Туринская — целочисленная. В целом, если событие имеет вероятность, большую чем фоновые события, то и по Палермской, и по Туринской шкале они имеют оценку, превосходящую 0. С другой стороны, события, имеющие оценку 1 по Туринской шкале, часто по Палермской шкале оказываются отрицательными, достигая по абсолютной величине нескольких единиц.