Адольф Эрман - Жизнь в Древнем Египте

а) 6/ 5х = 21

б) 6 х = 21 х 5

в) х = 2 1/ 6х 5

г) х = 3 1/ 2х 5

д) х = 17 1/ 2

Проверка: 17 1/ 2+ 3 1/ 2= 21

О геометрии египтяне знали еще меньше, чем об арифметике, хотя им было крайне необходимо умение измерять площадь участка поверхности из-за того, что каждый год разлив уничтожал очень много границ между полями. Все их расчеты имели в основе прямоугольник, площадь которого они верно определяли как произведение длин двух его сторон. Но, как ни странно, они совершенно не замечали, что нельзя обращаться одинаково со всеми четырехсторонними фигурами, у которых противоположные стороны имеют одинаковую длину. И поскольку египтяне рассматривали каждый четырехугольник как четырехугольник, у которого две стороны совпадают одна с другой, а две остальные вдвое короче этих, они переносили эту ошибку и в вычислительные операции над треугольниками. Кроме того, для них равнобедренный треугольник был равен половине произведения длин его длинной и короткой сторон, потому что они во всех случаях определяли площадь соответствующего ему четырехугольника как произведение длин двух его сторон, словно это был просто прямой угол. Ошибка, возникавшая из-за заблуждений такого рода, в определенных обстоятельствах могла быть велика.

Вычисление площади трапеции тоже страдало от этой ошибки: чтобы определить ее площадь, они умножали длину наклонной стороны на половину произведения длин двух параллельных сторон. Как мы видим, основной принципиальной ошибкой данных египетских учеников в деле измерения площадей было то, что они так никогда и не поняли значение перпендикуляра. Вместо него они пользовались одной из наклонных сторон и этим с самого начала лишили себя возможности работать правильно. Стоит отметить, что при таких ошибках они все же нашли правильный способ приблизительного вычисления площади круга; в этом случае они вычитали из диаметра его девятую часть, а остаток умножали сам на себя. То есть, если диаметр круга был равен 9 родам (здесь род – длина измерительного жезла, английская единица измерения. – Пер.), площадь круга, по их расчетам, была 8 х 8 = 64 квадратных рода, и этот результат отличался от верного всего лишь примерно на 2/ 3квадратных рода.

Среди задач на измерение объема, которые пытались решить египтяне, было, например, определение того, сколько зерна входит в амбар определенного размера. Судя по тому немногому, что мы в настоящее время можем более или менее ясно понять в этих задачах, основные концепции египтян в этом случае были верны, но условия задач слишком сложны, чтобы мы могли составить о них какое-то определенное мнение. Но если бы мы и понимали их, они, вероятно, мало изменили бы наше общее впечатление от математики древних египтян, и наше заключение по ее поводу таково: об их теоретическом знании этой науки сказать почти нечего, но их практические познания в ней очень хорошо удовлетворяли простые потребности повседневной жизни.

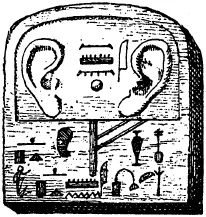
Маленькая стела, которую писец по имени Аменхотеп посвятил Амону-Ра, вероятно в благодарность за излечение больного уха (W. 358, из Фив)

Сказки всегда радовали сердца и современных, и древних египтян, и, когда ученый-первооткрыватель извлекал из тьмы сказочного фольклора феллахов настоящие сокровища, он сразу догадывался, что такие рассказы имеют очень древнее происхождение [334]. Действительно, от различных периодов египетской истории до нас дошло довольно много очень похожих по характеру рассказов; и это позволяет нам понять, какое огромное наслаждение египтяне находили в рассказывании историй. Эти легкие поэтические сочинения, несомненно, во все времена пользовались любовью у египетских крестьян, хотя, возможно, не всегда занимали столь же почетное место в египетской литературе. Мы ничего не знаем о состоянии этой литературы до эпохи Среднего царства, но несколько повестей этой эпохи дошли до нас, и их содержание свидетельствует об их народном происхождении. Интересный литературный отрывок, входящий в состав Берлинского папируса, тоже имеет, если можно так сказать, простонародный характер. В нем говорится о том, как молодой пастух на мгновение увидел среди болот богиню и сильно влюбился в нее. «Он никогда не говорил с ней, [но] ее власть преследовала его тело». Тогда по его желанию были прочитаны самые мудрые колдовские заклинания пастухов, и «когда рано на рассвете… он встал перед озером, она пришла к нему без одежды, ее волосы были в беспорядке» [335]. Что она сказала ему, читатель должен придумать сам, потому что, к несчастью, древний владелец этой книги посчитал нужным смыть с папируса и начало, и конец этого текста, чтобы дешево получить чистую бумагу [336].