• В некоторых случаях вы знаете, что костяшка должна занимать определенную клетку, но пока не можете определить ее направление, потому что эта клетка граничит с соответствующей парной цифрой с нескольких сторон. В этом случае очертите те границы клетки, в которых вы уверены, – это поможет ограничить варианты для соседних костяшек.
• Помните, что каждая нерешенная область должна содержать четное количество клеток, потому что костяшки состоят из пары клеток. Иногда это правило позволяет провести линии в определенных местах, что помогает с дальнейшим решением.
ПОПРОБУЙТЕ СВОИ СИЛЫ

Усложняем: разместите в сетке набор домино с количеством точек от 0 до 8.
+ Заполнить все клетки поля числами начиная с 1 (конечное число зависит от размера поля в головоломке)
+ Числа должны идти в порядке возрастания
ПРАВИЛА
Заполните все клетки поля числами от 1 (конечное число зависит от размера поля в головоломке). Числа должны быть размещены так, чтобы образовать непрерывный «путь» от 1 до наибольшего числа, возрастая на единицу в каждом шаге. Числа не должны повторяться. Разрешенные шаги соответствуют ходам короля в шахматах – то есть влево, вправо, вверх, вниз или по диагонали на соседние клетки.
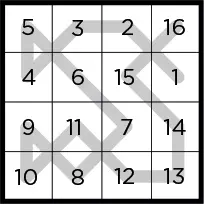
МЫСЛИТЕЛЬНЫЙ ПРОЦЕСС
В процессе решения этой головоломки часто надо делать догадки и корректировать их по мере дальнейшего решения, пока количество вариантов в каждой клетке не будет сведено до единственно возможного числа. Это отличный пример пошаговой оптимизации, когда первоначальное предположение постепенно уточняется и доводится до совершенства.

УЧЕБНЫЙ ТРЕНАЖЕР
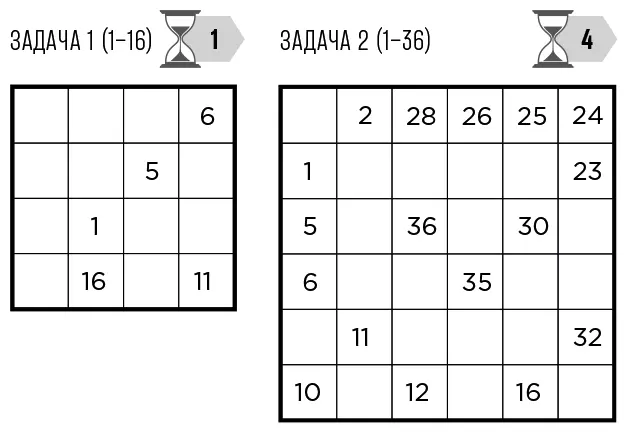
Нарисуйте «путь короля» от 1 до 16 в задаче 1 и от 1 до 36 в задаче 2.
• Чтобы определить начало и конец пути, обычно нужно поломать голову, но в задачах в этой главе они обозначены. Кроме начальной и конечной клеток, во всех остальных случаях путь должен входить в каждую клетку и выходить из нее. Поскольку угловые клетки и в меньшей степени клетки по краям более ограничены в вариантах, чем клетки в середине поля, решение головоломки лучше начинать с них, когда это возможно.
• Поищите числа, разделенные одним числом. Можно ли поместить число между ними в единственно возможную клетку?
• Также поищите числа, которые разделены максимально возможным количеством клеток, – например, числа, отстоящие друг от друга на три числа, между которыми находится три клетки. В этом случае путь должен пролегать по прямой от одного числа к другому. Однако чем дальше друг от друга отстоят числа, тем больше между ними возможных маршрутов. Вы можете проложить между ними предполагаемый путь (пометив, что это предположение, а не окончательный вариант) и, отталкиваясь от этого, работать дальше.
УЧЕБНЫЙ ТРЕНАЖЕР
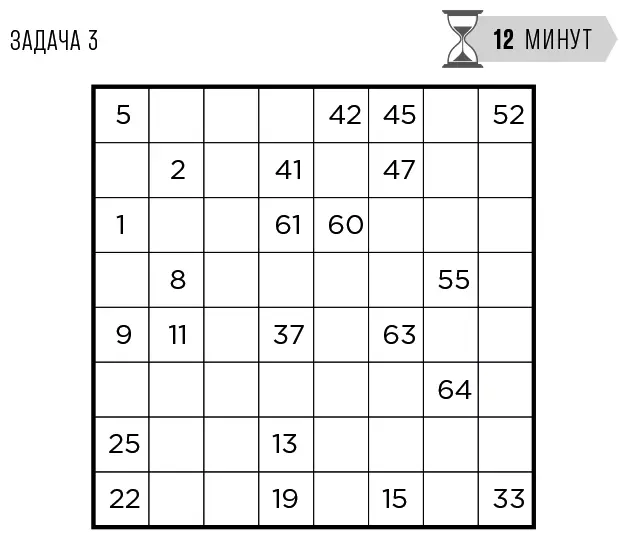
Разместите в сетке числа от 1 до 64.
• Помните, что король может двигаться по диагонали. Если забыть об этом, головоломка может показаться неразрешимой, тогда как из кажущегося тупика есть простой выход.
• Заполняя поле, постоянно проверяйте пустые клетки. Можно ли провести через них путь и, если да, будет ли он соединять числа в соответствии с правилами? Если нет, значит, нужно исправить те части пути, которые вы уже проложили.
• Если какая-то область поля вызывает затруднение, оставьте ее и займитесь другой – проложенная там часть пути может в итоге затронуть эту трудную область и подсказать ее решение.
ПОПРОБУЙТЕ СВОИ СИЛЫ
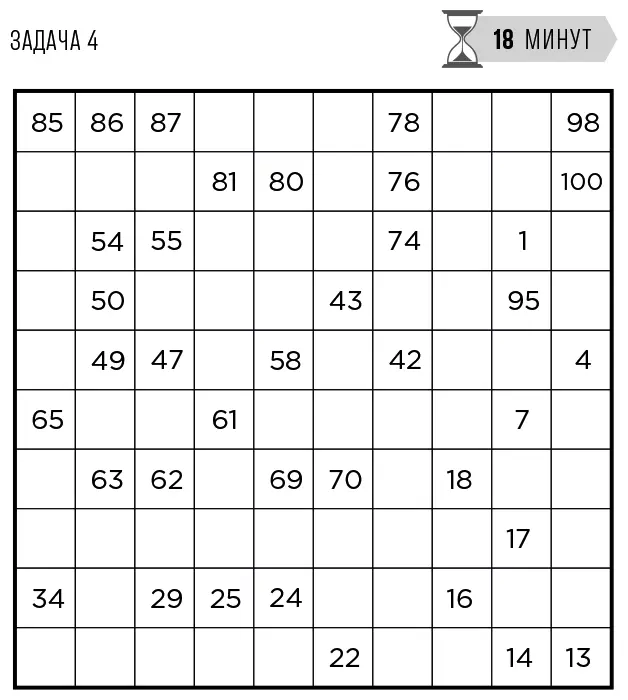
Разместите на поле числа от 1 до 100.
+ Найти путь от входа до выхода
Читать дальше


















