Ричард Нисбетт - Что такое интеллект и как его развивать. Роль образования и традиций

Иудейская культура, вне всякого сомнения, тоже благоприятствует интеллектуальному развитию. Евреи ценят любой успех вообще и интеллектуальные достижения в частности. Различия в интеллектуальных достижениях самого высокого уровня между евреями и неевреями очень велики. Объяснить их можно, не прибегая к генетике. В средние века наблюдались еще большие различия между арабами и китайцами с одной стороны и европейцами с другой, равно как и между разными государствами Европы на разных этапах их истории (в частности, смена ролей между Италией и Англией и переход Шотландии от варварства к интеллектуальным вершинам за какие-то двести лет), и до сих пор они существуют между различными регионами США. Разница в IQ между евреями и другими народами составляет 2/ 3СО. И по крайней мере частично этот разрыв связан с культурой.

Наконец, мы способны и сами сделать очень многое для того, чтобы повысить свой собственный интеллект и интеллект наших детей. Самые разные факторы — от биологических (физические упражнения и отказ от курения и употребления алкоголя во время беременности, грудное вскармливание новорожденных) до педагогических (обучение принципам классификации, следование продвинутым методикам воспитания) — могут оказывать влияние на интеллект.

Так что теперь можно смело отказаться от предрассудка наследственной трактовки интеллекта. Конечно, одна только вера в то, что наш интеллект — в наших руках, не сделает нас умнее. Но это прекрасное начало.

Любые явления можно схематически изобразить в виде кривой нормального распределения, изображенной на рисунке А1, имеющей колоколообразную форму. Например, если нам нужно представить в виде графика количество яиц, откладываемых ежедневно разными курами, число ошибок, возникающих при производстве разных типов автомобилей, или результаты IQ-тестов для группы людей, форма графика, представляющего эти данные, будет приближаться к колоколообразной. Нам нет надобности углубляться в математические обоснования того, почему графики распределения имеют такую форму. Важно то, что график нормального распределения помогает строить предположения о том, где будут находиться данные наблюдения относительно других данных. График нормального распределения на рисунке А1 разделен на области стандартных отклонений, называемых так потому, что норма представляет собой отклонение от среднего значения (примерно) на эту величину. При абсолютно нормальном распределении, которое является математической абстракцией, однако встречается достаточно часто при очень большом количестве данных, примерно 68% всех данных наблюдений попадают в область от +1 до -1 стандартного отклонения (СО) от среднего значения (которое на рис. А1 представлено нулевой точкой).

Кроме того, в концепции стандартного отклонения для нас полезно то, что касается отношений между процентильными значениями и стандартным отклонением. Примерно 84% всех наблюдений попадают в область значений, которые на 1 СО или менее выше среднего; наблюдения выше среднего ровно на одну величину СО находятся на 84-й процентили распределения. Оставшиеся 16% находятся за пределами одной величины стандартного отклонения. Почти 98% всех наблюдений попадают в область, равную или превосходящую среднее значение на 2 СО. Результат, превышающий среднее ровно на 2 СО, находится на 98-й процентили. Оставшиеся 2% результатов лежат выше. Практически все результаты наблюдений попадают в рамки от -3 до +3 СО. По договоренности СО в распределении результатов IQ-тестов принято считать равным 15 (при среднем значении, равном 100).

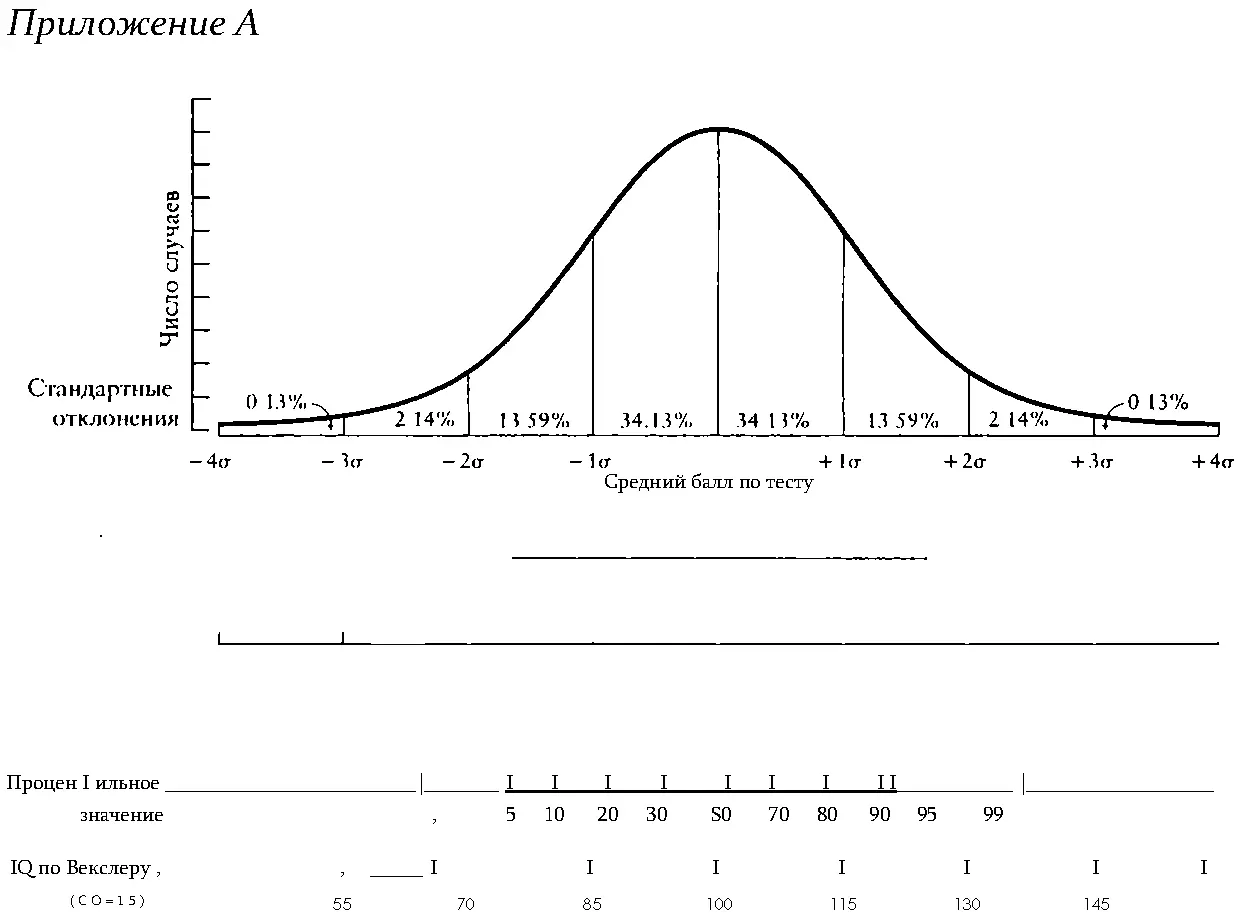
Рис. А1. Кривая нормального распределения, где стандартные отклонения от среднего отмечены вертикальными линиями, с соответствующими процентильными значениями и результатами IQ-теста Векслера, приведенными внизу. Обратите внимание, что 68% результатов попадают в область от -1 до +1 стандартного отклонения (σ) от среднего.

Стандартными отклонениями удобно пользоваться при описании размера эффекта, например, если нужно выяснить, какое влияние на знания учеников оказывает новая методика преподавания. Наиболее часто используемый в статистике индикатор размера эффекта — это так называемый параметр Коэна d, который рассчитывается следующим образом: из среднего значения для группы А вычитается среднее значение для группы В, и разность делится на среднее из стандартных отклонений двух групп (или иногда только на СО для группы А).