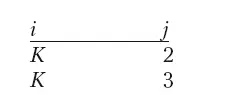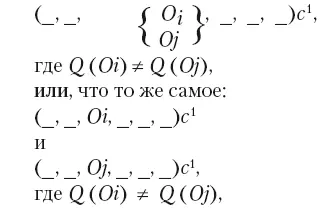Ричард Бендлер - Большая энциклопедия НЛП. Структура магии [litres]

Мгновенное описание считается плохо сформулированным, если:

( Ii , Rj , —, —, —, —),

где i № j .

В сущности, данное условие гласит, что нечеткие функции не считаются правильными. То есть, например, любое описание, в котором визуальная информация одновременно репрезентируется кинестетически, не будет считаться хорошо сформулированным описанием.

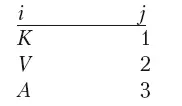
Ниже в левой колонке приведены плохо сформулированные мгновенные описания, а в правой колонке – правильные:

( V , K , _, _, _, _) ( V , V , _, _, _, _)

( A , K , _, _, _, _) ( A , A , _, _, _, _)

( A , V , _, _, _, _) ( K , K , _, _, _, _)

( K , A , _, _, _, _) ( D , D , _, _, _, _)

2. Мгновенное описание хорошо сформулировано, если:

(_, Ri , _, Sj , _, _),

где i и j составляют одну из приведенных ниже пар:

Все другие парные значения считаются в психотерапии неправильными.

3. Мгновенное описание хорошо сформулировано, если:

(_, _, Oi , Sj , _, _),

где значения i и j не составляют одной из приведенных ниже пар:

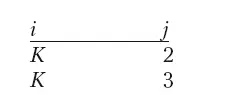
Отметим, что все остальные взаимоотношения не являются необходимым образом правильными, – они могут быть неправильными по отношению к значениям других переменных в шестикортежном векторе. Например, парные значения переменных S и О, создаваемые мгновенным описанием

(_, _, K , 1, _, _),

будут удовлетворять условию правильности № 3. Однако если переменная М будет иметь значение n, данное мгновенное описание будет плохо сформированным. Другими словами, хотя сочетание значений К и 1 для параметров О и S является правильным, тройка значений

(_, _, K , 1, _, n )

окажется неправильной. Мы понимаем, что три представленных здесь условия не исчерпывают условий правильности для шестикортежности. Мы предложили их в качестве примера того, каким образом может быть разработана полная модель множества правильных мгновенных описаний.

Ниже мы предлагаем два примера перевода техник, описанных в данном томе, в формальную систему обозначений, чтобы продемонстрировать, как вы можете использовать шесткортежность в качестве вспомогательного средства для организации своего психотерапевтического опыта. Множества мгновенных описаний могут оказать существенную помощь при работе с неконгруэнтностью, как в индивидуальной психотерапии, так и в контексте психотерапии семьи. В первом случае – индивидуальная психотерапия – шестикортежность позволяет определить понятия конгруэнтности и неконгруэнтности. Мы определяем функцию Q для множеств значений параметра O таким образом, что:

Q ( Oi ) = значение сообщения, передаваемого по выходному каналу Oi .

Имея функцию Q и мгновенное описание, мы можем определить неконгруэнтность как случай, когда имеется более одного входа для значения параметра O , так что, у одного и того же индивида:

Q ( Oi ) ≠ Q ( Oj ),

где ≠ значит «одно противоречит другому».

Другими словами, если у нас есть для данного индивида шестикортежная репрезентация, имеющая вид:

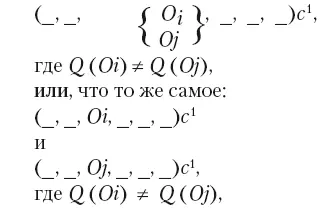
то индивид, обозначенный как c 1, неконгруэнтен. Если O i и O j представлены одновременно, то указанные шестикортежные репрезентации указывают на одновременную неконгруэнтность (случай, который мы подробно рассматривали в начале части II). Клиент предъявляет более одного сообщения, причем они не согласуются друг с другом, противоречат одно другому. Если приведенные выше шестикортежные репрезентации относятся к одному и тому же клиенту, но в разные моменты психотерапевтического сеанса, то мы имеем дело с последовательной неконгруэнтностью. Например, во второй фазе работы с неконгруэнтностью клиент будет представлен множеством мгновенных описаний, удовлетворяющих следующему условию:

Q ( O i ) ≠ Q ( O j )

для всех i и j .

На языке шесткортежности конгруэнтность представляет собой условие, которое выполняется, когда:

Q ( O i ) = Q ( O j ) = ...... = Q ( O k ) = ...... = Q ( O n )