Бо Лотто - Преломление. Наука видеть иначе

Революционные вопросы и начинающиеся с них кардинальные изменения, преобразования вырастают на руинах старых предположений: мы разрушаем их, чтобы построить новые, более разумные. Проблема лишь в том, что мы не видим, почему делаем именно то, что делаем. Как мы убедились, предположения, формирующие наше восприятие, часто похожи на воздух, которым мы дышим… они невидимы, поэтому трудно понять, в чем можно усомниться и где произнести «почему». В этой главе мы научимся видеть то, что скрыто от глаз.

Посмотрите на картинку: свечка, спички и коробочка с канцелярскими кнопками. Задача простая: вы должны прикрепить свечку к стене и зажечь ее, используя только предметы на картинке. Этот эксперимент называется «Задача Дункера» по имени ее создателя Карла Дункера (прошу не заглядывать вперед, чтобы найти ответ) [73] Вообще в задаче Дункера была идея прикрепить свечку так, чтобы воск не капал на пол. . Обратите внимание: острие у кнопок недостаточно длинное, чтобы проткнуть саму свечку.

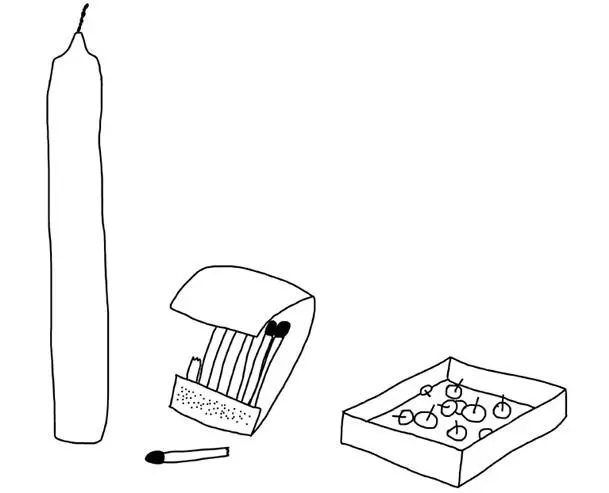
Сложно? Большинство людей считают задачу непростой, как и я, когда впервые ее увидел. Несмотря на то что «правильный» ответ ( X в поле возможностей), по существу, находится легко, многим требуется немало времени, чтобы найти решение, если они вообще его находят. Значит ли это, что мы не умеем мыслить творчески, поэтому не получается и соединить две несовместимые идеи, и полностью вовлечься в «таинственный, непредсказуемый творческий процесс»? Разве это свидетельствует о том, что у нас не хватает генов, которые есть у тех немногих, кто способен сделать большой шаг в неизвестное?

Не забывайте, что ландшафт вашего поля возможностей определяется вашими предположениями. Рисунок рельефа создан таким образом, чтобы позволить определенные допущения, а следовательно, схемы активности в мозге (аттракторы), с большей вероятностью, чем другие. Аналогично: посмотрите на рисунок куба выше (к свечке мы вернемся чуть позже). Верхняя грань кубообразной фигуры темная, а нижняя — светлая, и между ними есть разница. Заметьте, что свет падает сверху и расположение граней относительно друг друга и разница цветов согласуются с освещением, хотя мы и не осознаём этого. Обратите внимание: предположение, что свет падает сверху, вшито в наш мозг, потому что это естественные условия на Земле, где мы прошли эволюционное развитие. Этот рисунок (в частности, цветовой градиент между гранями) я создал, изучая с Дейлом Первсом иллюзию Корнсвита [74] Иллюзия Корнсвита была выявлена в 1960 году психологом Томом Корнсвитом. Он известен благодаря исследованиям визуального восприятия: открыл, что люди воспринимают цвет и оттенок объемного изображения в зависимости от освещенности и теней. . И я так его организовал, чтобы подкрепить ваши предположения и активировать определенные нейронные пути у вас в голове. В результате вы, как я и задумывал, увидели две грани так, будто они освещены по-разному.

Да, с точки зрения физики поверхности идентичны . Они одного и того же цвета.

Если не верите, посмотрите на картинку выше, где отдельно выделены центральные области двух поверхностей. Еще можете перевернуть книгу вверх ногами, тогда картинка перестает выглядеть так, будто свет падает сверху. Когда это происходит, иллюзия становится слабее, так как теперь раздражитель в меньшей степени согласуется с вашими предположениями относительно верхнего освещения.

То, что справедливо для куба, аналогично и в творческой задаче со свечкой и спичечным коробком. Точно так же как вы не можете разглядеть реальный цвет поверхностей граней куба, вы не в силах придумать правильное решение задачи со свечкой… потому что воспринимаете его с точки зрения наиболее вероятных предположений, лежащих в поле ваших возможностей. Но если изменить эти допущения, вы трансформируете восприятие в будущем, как в случае с вращающимся октаэдром. Эту задачу трудно решить не из-за сложности, а скорее потому, что вы не видите предположений, которые, по задумке автора, должны активироваться у вас в голове. Если бы вы знали, что это за гипотезы, мгновенно нашли бы выход. И если базироваться на новых предположениях, требующихся для решения задачи, то этот вариант был бы самым очевидным.