Роберт Фрэнк - Успех и удача [Фактор везения и миф меритократии] [litres]

Роль удачи в таких состязаниях аналогична влиянию ветра на результаты соревнований по легкой атлетике. Установление мирового рекорда в легкой атлетике является спортивным достижением высшего порядка. Все без исключения спортсмены, которым это удавалось, от рождения обладали почти сверхчеловеческими талантами и трудолюбием, что позволило им выдерживать долгие годы изнурительных тренировок. Однако даже здесь важную роль играет случай. Чтобы вы смогли установить рекорд, все условия должны совпасть едва ли не идеально.

В четырех видах соревнований по легкой атлетике – забег на 100 метров, бег с препятствиями на 110 метров (для женщин – на 100 метров), прыжок в длину и тройной прыжок – результаты зависят (немного, но ощутимо) от наличия встречного или попутного ветра. Поэтому руководящие международные спортивные органы постановили, что мировые рекорды могут регистрироваться лишь в ходе соревнований при скорости попутного ветра не более двух метров в секунду.

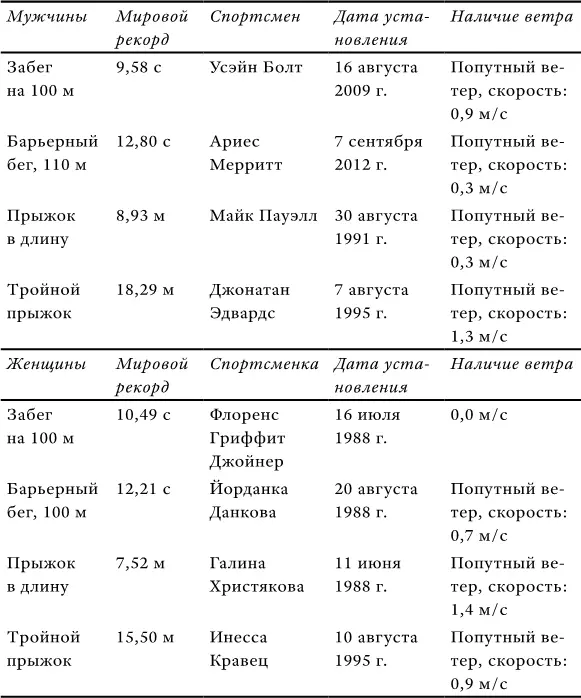
В табл. 4.1 обращает на себя внимание тот факт, что из восьми ныне действующих мировых рекордов семь были установлены при наличии попутного ветра, и ни одного – при встречном ветре. Семь из восьми предыдущих рекордсменов также побеждали при попутном ветре (единственным исключением оказался забег на 100 метров у мужчин, где не было ни встречного, ни попутного ветра) [18] См.: List of World Records in Athletics // Wikipedia. ‹ http://en.wikipedia.org/wiki/List_of_world_records_in_athletics#Men › and ‹ http://en.wikipedia.org/wiki/Athletics_record_progressions ›. .

Одним из способов оценки того, как случайные события влияют на результаты состязаний, является численное моделирование. С его помощью изучается ряд предположений относительно того, в какой степени фактор удачи влияет на результаты. Численное моделирование, широко используемое как в общественных, так и в естественных науках, помогает исследователям лучше понять сложные интерактивные процессы.

Таблица 4.1

Роль ветра в установке мировых рекордов в соревнованиях по легкой атлетике

Вернемся к знакомому вопросу: какова вероятность того, что, когда вы бросаете монетку, «орел» выпадет 20 раз подряд? Тот, кто знаком с основами теории вероятностей, легко решит подобную задачу [19] Поскольку вероятность того, что при бросании монетки выпадет «орел», составляет 1/2, вероятность того, что это произойдет 20 раз подряд, определяется как (1/2) 20 , что составляет 0,0000095367. . Однако для многих сложных проблем подобные решения невозможны. В таких случаях альтернативным способом действия бывает многократное моделирование предполагаемых условий и наблюдение за частотностью событий. В эксперименте с монеткой теоретически можно привлечь армию из миллиарда добровольцев, которые бросили бы монетку 20 раз подряд. Затем следовало бы подсчитать вероятность, с которой «орел» выпадает 20 раз подряд, как долю из того миллиарда попыток, которые были для этого предприняты.

Армия добровольцев нам, конечно, не понадобится, поскольку компьютер можно легко запрограммировать на моделирование результатов, ожидаемых в ходе подобного эксперимента. Именно этим методом я пользуюсь для оценки того, сколь значим фактор удачи в исходе соревнований с большим числом участников, где «победитель получает все».

В Приложении 1 описаны несколько примеров такого моделирования. Подобно состязаниям по легкой атлетике, все они имеют форму конкурса, где «победитель получает все», а исход зависит лишь от личной эффективности. Эффективность поддается объективному измерению, и конкурс выигрывает тот, у кого совокупное число баллов окажется наибольшим. Эффективность, в свою очередь, зависит от личного сочетания таланта, усилия и удачи.

В одном из случаев моделирования рассматривается базовый пример конкурса с участием 100 тыс. человек, где доля удачи в совокупной эффективности составляет лишь 2 %. Остальные 98 % эффективности в равных долях обеспечиваются усилиями и талантами участников. Показатели талантов, усилий и удачи каждого участника определяются независимым выбором случайных чисел, находящихся в диапазоне от 0 до 100. В данном сеансе моделирования средний балл победителей конкурса составлял 90,23, причем в 78,1 % случаев победители не обладали максимумом талантов и усилий. В большинстве случаев находился ряд участников, чьи показатели таланта и усилий оказывались выше, чем даже у победителя.