Барбара Тверски - Ум в движении [Как действие формирует мысль] [litres]

Математические обозначения были и остаются чрезвычайно важными во всех аспектах повседневной жизни. Как вы помните из главы 7, люди, подобно многим другим животным, владеют системой приблизительных количеств, позволяющей интуитивные оценки и сравнения в случаях, когда оба комплекса объектов можно видеть. Однако эта система является не только примерной, но и логарифмической, т. е. в ней одна и та же разница между малыми числами более весома, чем между большими. Это относится к суждениям не только о количестве, но и о яркости, громкости и многом другом. Исправить подобные ошибки можно с помощью системы точных чисел, позволяющей измерять и вычислять. До сих пор существуют культуры, не знающие числа, да и современной культуре потребовались столетия, чтобы создать изощренную систему, сегодня доступную даже школьникам. Удивительно, что эволюция не уничтожила широко распространенных систематических ошибок оценочной системы человеческого ума. Без сомнения, система приблизительных количеств была полезна нам как-то иначе. К добру или к худу – истина всегда такова – это не единственные систематические ошибки ума человека. Некоторые, но никоим образом не все, можно исправить или уменьшить при помощи измерений и вычислений.

Как много всего мне не пришлось даже упомянуть! Потрясающие достижения систем обозначений в сферах математики, логики, физики, химии, статистики и многих других. Геометрию, смешанную систему: отчасти буквально пространственную, отчасти абстрактно пространственную, отчасти символическую. Интересно, что для Евклида доказательства имели вид схем, текст лишь озаглавливал их. К сожалению, оригинальные схемы были утрачены.

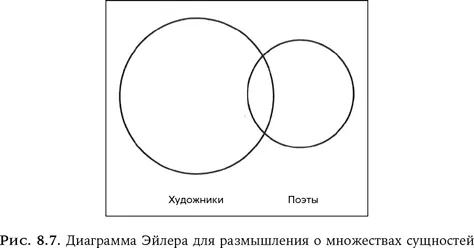
Одним из инструментов логики являются диаграммы Эйлера – круги, представляющие множества вещей, где пересекающиеся круги обозначают пересекающиеся множества, отдельные – отдельные, непересекающиеся множества, а включенные друг в друга – включения. Даже слова совпадают. Подумайте, сколько выводов можно сделать из простой диаграммы Эйлера на рис. 8.7. Каждый круг представляет множество каких-то сущностей, например художников и поэтов. Частичное наложение, которое называется пересечением двух множеств, указывает на тех, кто является одновременно и художником, и поэтом. Вне кругов находятся все, кто не относится ни к тем ни к другим.

Из этой диаграммы напрашивается несколько выводов: некоторые художники – поэты, некоторые поэты – художники, некоторые художники не поэты, не все поэты художники и т. д. Такие отношения из диаграммы очевидны. Она делает наглядными безжизненные формулировки, и их несравненно легче воспринимать, чем словесные утверждения. Есть множество надежных свидетельств, что люди могут строить пространственные мысленные модели на основании ясных (правильно составленных!) текстов, но это требует времени и усилий. Диаграммы Эйлера экономят силы.

Ученые решили не ограничиваться априорными заявлениями о превосходстве диаграмм Эйлера над утверждениями, однако эмпирические данные оказались смешанными. Вероятно, репрезентации конфликтуют с процессами рассуждений, которые развертываются последовательно, по частям. Визуализация показывает все отношения одновременно; для больших множеств отношений трудно выделить части, отдельные предположения, которые использовались бы как аргументы. Список утверждений справляется с данной задачей, он разделяет полное множество отношений на дискретные части. Представляется, что это очередной пример, когда Принцип использования перевешивает Принцип соответствия.

Это удобство логического мышления с помощью грамотно составленных диаграмм и схем вызвало бурный рост новых областей знания, пытающихся сделать подобные изображения основой математики, логики, физики и компьютерных наук без утраты их строгости, – чтобы задействовать нашу потрясающую способность видеть пространственные отношения и мыслить о них. Логика здесь та же: схемы используют возможности пространственно-двигательного мышления для абстрактного. Марк Векслер [58] Настоящее имя исследователя – Марк Евгеньевич Веклеров. Он родился в Москве в 1967 г. – Прим. ред. , ныне исследователь когнитивных процессов, изучающий восприятие и ментальную образность, когда-то был физиком и работал с диаграммой Фейнмана, представленной на рис. 8.8. Каждый серый пузырь представляет отдельную вселенную. Чтобы вселенные были скоординированы, нужно устранить перекручивание нижнего пузыря. Векслер представил, как берет каждый из нижних эллипсов большим и указательным пальцами и крутит их в противоположных направлениях, словно играя в «веревочку». Сделав это, он понял, что раскручивание нижнего пузыря скручивает верхний. Единственный способ избежать скрутки – перерезать одно из прикреплений. Этот вывод имеет следствия для пространственно-временного континуума и квантовой гравитации, но они вне моего понимания и, к счастью, вне темы книги. Интуитивная догадка исследователя оказалась верной, что он впоследствии и подтвердил с помощью точного построчного доказательства.