Барбара Тверски - Ум в движении [Как действие формирует мысль] [litres]

Реальное вращение помогает мысленному, однако, физически двигаясь прямо вперед или назад, мы, судя по всему, не помогаем себе вообразить движение вперед или назад. Вращение же в пространстве вызывает радикальные изменения пространственных отношений окружающих нас вещей: то, что было вверху, может оказаться справа, а объект, бывший слева, теперь очутился сзади. Копирование движения явно помогает нам обновлять эти пространственные отношения. Движение вперед или назад – перенос в пространстве – может изменить то, что впереди и сзади, но не меняет того, что справа и слева. Обновление пространственных отношений при воображаемом переносе, очевидно, не представляет трудностей и не выигрывает от подспорья в виде реального движения.

Все это указывает на сложность мысленного вращения, будь то собственное тело или объекты у нас перед глазами, а также на роль соответствующих действий тела в поддержке этого мышления.

Мысленное вращение вызвало огромное воодушевление в научном мире и породило другие замечательные исследования пространственного мышления. Если ум может представить вращение, на какие еще чудеса он способен? Можем ли мы вообразить, как предметы меняют размер, местоположение, форму? Или добавить к ним части, удалить, перекомпоновать их? Можем ли внимательно рассмотреть их, чтобы вынести суждение, например о величине и расстоянии? Да, люди с большей или меньшей легкостью выполняют эти и многие другие мысленные манипуляции. Попробуйте сами. Представьте себе половину грейпфрута выпуклой стороной вверх, плоской вниз. Теперь вообразите, что подвешиваете к середине плоской части заглавную букву J . Что у вас получилось?

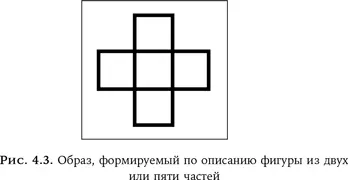
Вы только что построили нечто у себя в голове из словесного описания без каких-либо визуальных входных данных. Мысленное конструирование, как и физическое, оказалось пошаговым процессом. Соответственно, чем больше частей, тем дольше оно длится. Например, фигуру на рис. 4.3 можно описать как состоящую из двух частей (двух пересекающихся прямоугольников) или пяти частей (пяти квадратов, сгруппированных определенным образом). Фигура одна и та же, но, если описывать и воспринимать ее как имеющую две части, построение образа в уме требует меньше времени, чем при описании и восприятии ее как пятичастной.

Мысленное конструирование повторяет физическое и в том, что это пошаговый процесс собирания из частей. Однако аналогия является более глубокой. Сначала выполните другое задание, знакомое из начальной школы, на геометрические аналогии. Попробуйте решить задачу, представленную на рис. 4.4.

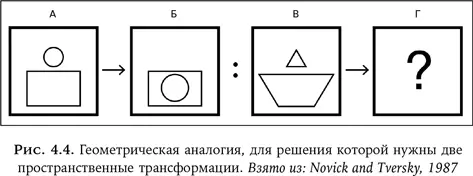
Для решения необходимо передвинуть маленькую верхнюю фигуру (круг или треугольник) внутрь большей нижней (прямоугольника или трапеции) и увеличить ее. Можно, наоборот, сначала изменить размер меньшей фигуры, а затем сместить ее в большую. Порядок выполнения действий неважен, как и при сложении ряда чисел.

Мы предлагали испытуемым подобные задачи на геометрические аналогии. В каждой требовалось осуществить две или три трансформации из большего набора возможных трансформаций. После решения каждой задачи участники исследования сообщали, в каком порядке они их производили. Хотя испытуемые были вольны выбрать любой порядок, их предпочтения совпадали: почти все следовали одному и тому же. Затем мы предложили другой группе выполнить трансформации либо в этом предпочитаемом порядке, либо в каком-то другом. Когда студенты второй группы использовали предпочитаемый порядок, то действовали быстрее и точнее. Поскольку математика не налагает никаких ограничений на порядок выполнения трансформаций, такие ограничения должны быть когнитивными, и мы задумались над этим вопросом. Возможно, испытуемые делали более трудные задания сначала, пока им было на что смотреть, а потом переходили к более простым, которые следовало выполнять полностью в уме. Итак, мы спросили участников исследования, какие трансформации дались им труднее, а также замерили, какие отнимают больше времени – это еще один показатель сложности. Красивая идея, но результаты ее не подтвердили. Тестируемые предпочитали сначала передвигать , затем поворачивать или отражать , затем удалять мелкую часть, затем добавлять половину [35] Здесь имеется в виду зеркально приставить такую же. См. иллюстрации к работе Novick and Tversky, 1987, упомянутой в разделе «Библиография». – Прим. ред. или менять размер , затем затемнять / покрывать штриховкой и наконец добавлять мелкую часть . Самой быстрой и простой трансформацией была первая ( передвигать ), а самой медленной и трудной – вторая ( поворачивать или отражать ). Итак, ни время, ни трудность задания не объясняли порядок действий. Мы по-прежнему ничего не понимали.