Малкольм Гладуэлл - Гении и аутсайдеры [Почему одним все, а другим ничего?]

Несколько лет назад Алан Шонфельд, профессор математики из Калифорнийского университета в Беркли, записал на видео, как женщина по имени Рене пытается решить математическую задачу. Ей лет двадцать пять. У нее длинные черные волосы, она носит круглые очки в серебристой оправе. На видео Рене работает с программой по обучению алгебре. На экране видны две оси: x и y. Программа просит ввести нужные координаты, а затем проводит по заданным координатам линию. Таким образом, если вы введете 5 на оси x и 5 на оси y, то получите следующее:

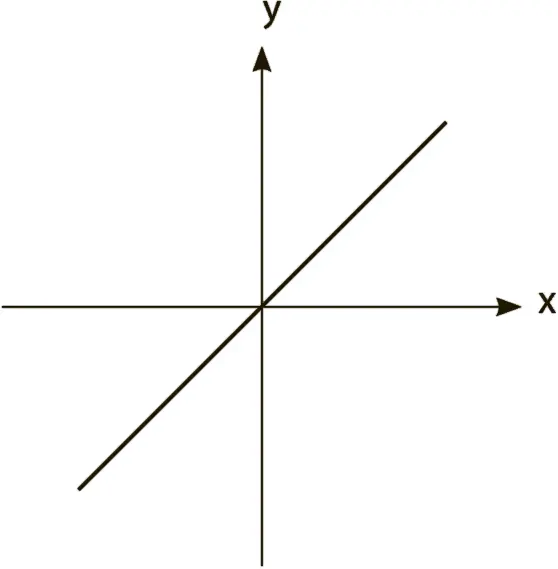
Подозреваю, где-то в глубине вашей памяти забрезжили смутные воспоминания об уроках алгебры в средней школе. Но будьте уверены, нет нужды вспоминать школьную программу, чтобы оценить важность примера на видео. Читая запись монолога Рене, думайте не о том, что, а о том, почему и как она говорит.

Компьютерная программа, разработанная Шонфельдом, позволяет студентам учиться рассчитывать угловой коэффициент. Угловой коэффициент – как, я уверен, вы помните (или, точнее сказать, уверен, вы не помните, во всяком случае, я не помнил) – есть отношение противолежащего катета к прилежащему. Угловой коэффициент равен 1, поскольку интервал изменения абсциссы равен 5 и интервал изменения ординаты также равен 5.

Итак, Рене сидит за клавиатурой и пытается сообразить, какие числа нужно ввести, чтобы программа нарисовала абсолютно вертикальную линию, совпадающую с осью y. Те, кто еще помнит уроки математики, понимают, что это в принципе невозможно. У вертикальной линии «неопределенный» угловой коэффициент. Ее интервал изменения ординаты бесконечен: любое число на оси y, начиная с нуля и до бесконечности. А интервал изменения абсциссы на оси x равняется нулю. Бесконечность, поделенная на нуль, не является числом.

Но Рене и не догадывается, что она пытается решить задачу, у которой нет решения. По выражению Шонфельда, девушка пребывает в блаженном заблуждении. Профессору особенно нравится показывать эту запись, поскольку она наглядно демонстрирует, как Рене постепенно выходит из этого заблуждения.

Рене – медсестра. Она никогда прежде не интересовалась математикой и на работе ни имела с ней дела. Но случайно получив доступ к этой программе, уже не может от нее оторваться.

– Я хочу провести прямую линию, параллельную оси y, – начинает девушка. Шонфельд сидит рядом с ней. Рене взволнованно смотрит на него. – Я уже пять лет всем этим не занималась.

Она принимается экспериментировать, вводя различные числа.

– Если я изменю угловой коэффициент вот так… минус один… Мне нужно сделать эту линию прямой.

Линия на экране монитора меняется в зависимости от вводимых чисел.

– Ой, так не получается.

У Рене удивленный вид.

– Что ты хочешь сделать? – спрашивает ее Шонфельд.

– Я хочу провести линию, параллельную оси y. Что мне для этого нужно? Кажется, мне нужно что-то изменить вот здесь (она показывает на рамку, куда вводится число для оси y). Вот что я поняла: если ты ставишь вместо единицы двойку, то график резко меняется. Так, если мне нужно подняться выше, нужно менять дальше.

Это и есть «блаженное заблуждение» Рене. Она установила, что чем выше координата на оси y, тем больше поднимается линия. Из чего она делает вывод: вертикальную линию можно нарисовать, введя достаточно большую координату на этой оси.

– Думаю, двенадцати или тринадцати будет достаточно. А может быть, даже пятнадцати.

Она хмурится, пытаясь вместе с Шонфельдом разобраться, что к чему. Задает ему вопросы. Он осторожно подталкивает ее в нужном направлении. Она предпринимает одну попытку за другой, пробует один вариант за другим.

В какой-то момент она вводит 20. Линия немного поднимается.

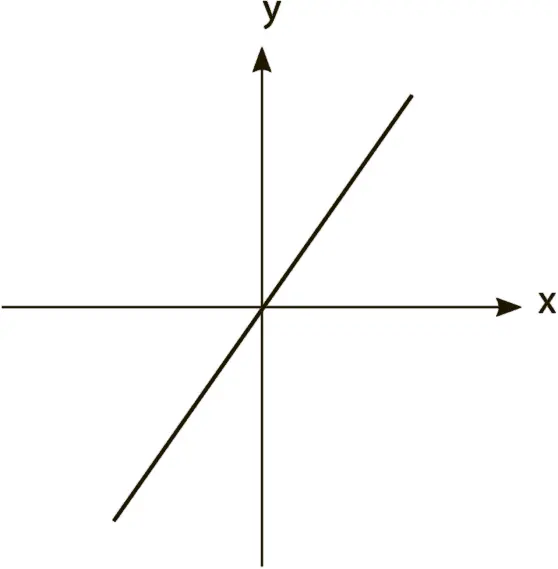
Она вводит 40. Линия поднимается еще выше.

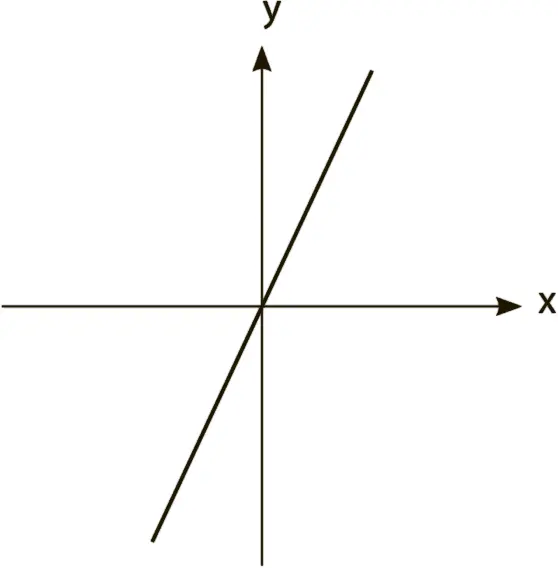
– Тут есть очевидное соотношение. Но никак не могу сообразить, что к чему… А если я введу восемьдесят? Если при сорока линия поднялась наполовину, тогда при восьмидесяти она должна подняться точно до оси y. Посмотрим, что у нас выйдет.

Она вводит 80. Линия поднимается еще выше, но все еще не вертикальна.