Василий Чибисов - Вся фигня – от мозга?!

Получается, что у нейрона множество входов и выходов? Не получается. У нейрона один выход и один вход. А как же множество связей? А так: все входящие сигналы суммируются, и уже в зависимости от суммы нейрон подаёт на выход какой-то новый сигнал. Или не подаёт. Но выходной сигнал у нейрона один, он бежит по одномуаксону и одинаковыйдля всех выходных контактов. А вы как хотели? Чтобы нейрон ещё разбирался, кому и что он отправляет? Нет, это уже дело получателей — блокировать или усиливать входящий сигнал с помощью медиаторов.

Ну хорошо, а зачем вообще нейронам сигналы? Затем, что электрохимические потенциалы — это единственная форма информации (энергии), распространяющейся по сети. Если нейрон как следует потормошить, по его дендритам начинает бежать электрический ток. Точные исследования показывают, что это не постоянное напряжение, а сложная последовательность всплесков. Нейрон буквально верещит, генерируя электрохимические бёрсты и спайки (рис. 2.2).

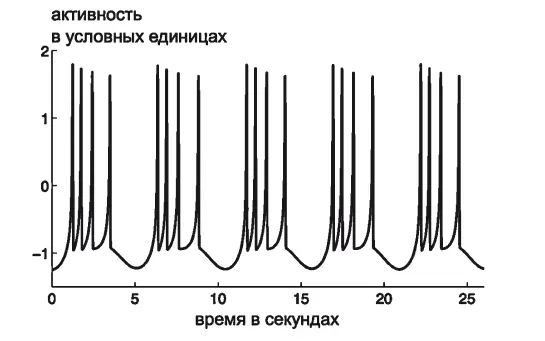
Рис. 2.2. Бёрсты и спайки искусственного нейрона в модели Хиндмарша — Роуз [1] Источник : Hindmarsh J. L., and Rose R. M. (1984) A model of neuronal bursting using three coupled first order differential equations. Proc. R. Soc. London, Ser. B 221:87–102.

Но нам не важно, какая форма у нервного сигнала. Важно, что другие нейроны одинаково реагируют на этот сигнал, воспринимая его как (простите за тавтологию) сигнал к действию. То есть напряжение с дендритов нейрона передаётся на аксоны «подконтрольных» нейронов. Аксоны, в свою очередь, получают сигналы от множества нейронов. Все сигналы, попавшие на аксон, суммируются на входе нейрона. И если сумма достаточно большая, то уже новый нейрон начинает верещать.

Теперь немного упростим и немного усложним картину. На рисунке 2.3 для удобства нейрон изображён кружочком. Аксон и дендриты вообще заменены на линии. Этот минималистский стиль активно используется в математической теории нейронных сетей, в схемотехнике, в теории графов… Короче, в любой технической дисциплине, когда нужно отвлечься от деталей и ухватить суть, прочувствовать саму архитектуру сложной системы.

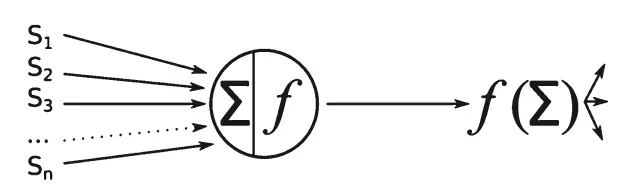
Рис. 2.3. Упрощенная схема суммирования сигналов в нейроне. Сумма входящих подставляется в функцию активации. Результат подается на единственный выход, где его уже ждут благодарные нейронные соседи

Мы видим, как несколько, а именно произвольное число n (подставьте на его место возраст соседского кота), сигналов поступают на вход круглого чёрного ящика. Там сигналы складываются (знак суммы) и сравниваются с пороговым значением. Если порог преодолён, нейрон выдает на выходе единицу. Иначе — ноль.

Функция f , имеющая форму ступеньки и превращающая входной сигнал в выходной (рис. 2.4), называется функцией активации. Само слово «функция» здесь употребляется в непривычном для многих значении. Обычно функция какого-то объекта — это его способности или предназначение. Например, функция паяльника — нанесение расплавленного припоя в место контакта деталей. В особых случаях — терморектальный криптоанализ. Но в нашем контексте функция — это математическая операция, превращающая одно число в другое (одно числовое множество в другое).

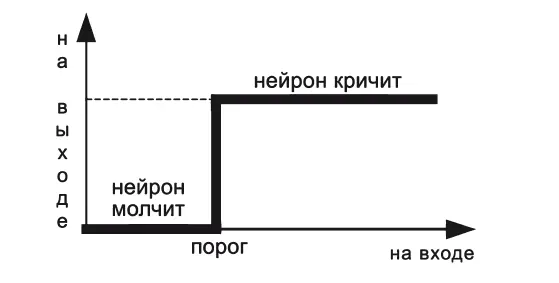
Рис. 2.4. Функция активации, то есть зависимость исходящего сигнала (вертикальная ось) от суммы входящих (горизонтальная ось)

Простейший вид функции активации — ступенька. Если число на входе меньше порогового значения U, то функция превратит это число в ноль. Если больше порога, то в единицу. Так вся бесконечная числовая ось отображается в две точки: ноль или один. Удобно, не правда ли? Удобно, но возникает несколько вопросов.

Почему ноль — понятно. Но вот почему именно единица? Почему не корень из двух, почему не минус сто, почему не потенциал ионизации атома водорода? Да потому что сравнивать не с чем. Все нейроны одинаковые. Эталон сигнала мы выбираем сами. Так что мешает положить максимально возможный сигнал равным единице? Ничего не мешает. Вот мы и кладём. Чтобы считать было легче.

А почему, либо ноль, либо единица? А если порог почти-почти преодолён? Или сумма входных сигналов застыла прямо на пороге? Направление вашей мысли понравилось бы любому специалисту по нейронным сетям. Чем дальше в лес, тем более хитрые зависимости выходного сигнала от входного придумывали учёные. Вместо ступеньки теперь часто рисуют «сигмоиду» — такую гладенькую возрастающую выпуклую кривую (рис. 2.5), прижимающуюся к единице по мере возрастания входного сигнала. То есть нейрон как бы верещит, но не громко.