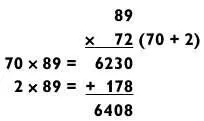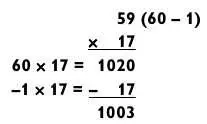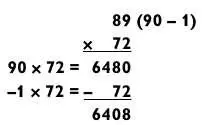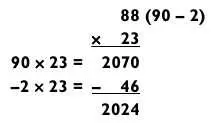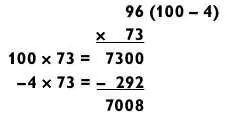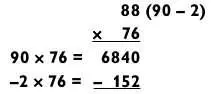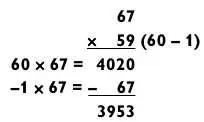Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

Следующую задачу вначале бывает очень трудно решить.

Попытайтесь умножить 89 х 72 в уме, подглядывая в случае необходимости в решение. Если вы справились с ней за две попытки, то все в порядке.

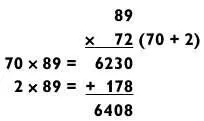
Если вы получили правильный ответ с первого или второго раза, похлопайте себя по плечу. В действительности не найдется задач на умножение типа «2 на 2» труднее этой.

Если вы не получили ответ сразу, не волнуйтесь. В следующих двух разделах я обучу вас более простым стратегиям для решения подобных задач. Но прежде чем продолжить чтение, попрактикуйтесь в методе сложения на следующих задачах на умножение.

Метод вычитания

Метод вычитания может пригодиться, когда одно из умножаемых чисел заканчивается на 8 или 9. Следующий пример показывает, что я имею в виду.

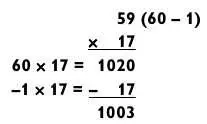
Хотя большинство людей находят, что сложение легче вычитания, порой удобнее отнять маленькое число, чем прибавить большое. (Если бы мы решали эту задачу методом сложения, то пришлось бы складывать 850 + 153 = 1003.)

Теперь рассмотрим сложную задачу, приведенную в конце предыдущего раздела.

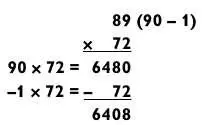
Разве это не намного проще? А вот задача, где одно из чисел заканчивается на 8.

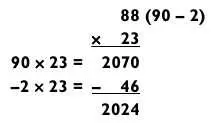
В данном случае следует поступить с числом 88 так: вычитаем 90 — 2, затем умножаем 90 х 23 = 2070. Но мы умножили с лишком. Каким? Он равен 2 х 23 = 46. Так что для получения ответа 2024 надо вычесть 46 из 2070.

Хочу подчеркнуть, что важно решать такие примеры в уме, а не просто изучать, как это делается. Пропускайте через себя эти задачи, проговаривайте выполняемые действия вслух, чтобы подкрепить свои размышления.

Я использую метод вычитания не только для чисел, оканчивающихся на 8 или 9, но и для чисел, близких и больших 90, поскольку 100 — очень удобное число для умножения. Например, если кто-то попросит меня умножить 96 на 73, я незамедлительно округлю 96 до 100.

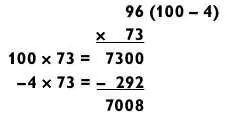
Когда действие на вычитание внутри задачи на умножение требует держать числа в уме, использование дополнений (которые мы изучили в главе 1) ускорит получение ответа.

Вы поймете, о чем я говорю, когда поработаете над задачами, приведенными ниже. Например, вычтите из 340 число 78.

Нам известно, что ответ будет в области «200 плюс». Разность между 40 и 78 составляет 38. С помощью дополнения к 38, которое равно 62, получаем ответ 262!

Теперь следующая задача.

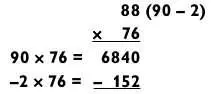
Есть два пути вычитания внутри данной задачи. Длинный путь состоит из вычитания 200 и прибавления 48.

Короткий путь заключается в понимании того, что ответ будет равен 6600 и «сколько-то еще». Для определения этого «сколько-то» вычитаем 52–40 = 12, а затем находим дополнение для 12, которое равно 88. Следовательно, ответ — 6688.

Попробуйте решить такой пример.

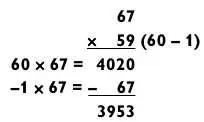
Снова идем коротким путем, взяв за основу ответ 3900 и сколько-то еще. Так как 67–20 = 47, а дополнение для 47 — это 53, ответ — 3953.

Как вы, наверное, поняли, использование данного метода возможно в любой задаче на вычитание, в которой требуется держать числа в уме, а не только тогда, когда она является частью решения задачи на умножение. Все это служит еще одним доказательством того (если вам нужны доказательства), что дополнение — очень мощный инструмент в математической магии. Освойте эту технику, и довольно скоро люди начнут рассыпать вам комплименты!