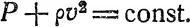
Рис. 2.При течении жидкости по трубе переменного сечения наименьшее давление будет в наиболее узкой части трубы
Почему так происходит? В чем причина такого, на первый взгляд, парадоксального явления?
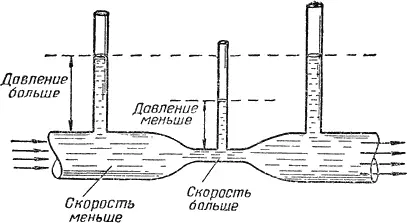
Рассмотрим уравнение Бернулли, которое в упрощенном виде можно записать так:
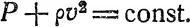
Здесь Р — давление, ρ — плотность жидкости, v — скорость. Обозначение const указывает, что это некоторая постоянная величина («константа»).
Для того чтобы сумма этих двух слагаемых оставалась постоянной, необходимо, чтобы при уменьшении (или увеличении) одного из этих слагаемых другое слагаемое увеличивалось (или уменьшалось) на такую же величину.
Поскольку плотность жидкости — величина постоянная (жидкость почти несжимаема), то увеличение скорости ее течения должно уменьшать давление, и наоборот. Уравнение Бернулли выведено с помощью высшей математики; оно основывается на законе непрерывности течения и законе сохранения массы.
Эффект уменьшения давления в жидкости при увеличении скорости течения можно наблюдать, если в струю воды, направленную вверх, поместить легкий пробковый шарик. Такой шарик будет все время «стараться» находиться ближе к центру струи, где скорость ее течения максимальна, за счет давления со стороны более медленно движущихся слоев воды на границе струя — воздух.
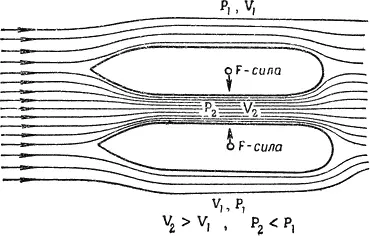
Рис. 3.При движений двух судов вблизи друг друга они притягиваются
Такой ка первый взгляд «безобидный» эффект может привести к далеко не столь безобидным результатам. Известны случаи, когда два судна, движущиеся параллельным курсом на небольшом расстоянии друг от друга, сталкивались между собой вследствие того, что скорость потока воды между ними оказывалась больше скорости потока вне их. Такое увеличение скорости движения жидкости между судами объясняется тем, что «ворота» между кораблями, в которые должна пройти вода, сужаются и поэтому нужна большая скорость, чтобы всей массе воды пройти сквозь более узкие «ворота» (рис. 3).
Используя уравнение Бернулли, Н. Е. Жуковский, С. А. Чаплыгин и другие ученые создали теорию подъемной силы крыла самолета.
Запросы техники, которая стала особенно стремительно развиваться в начале XIX.в., привели к созданию новых отраслей гидромеханики, и в частности гидромеханики вязкой жидкости, теории так называемого пограничного слоя, который образуется перед носовой частью тела, движущегося в жидкости или газе. В дальнейшем теория пограничного слоя получила применение в расчетах, связанных с движением сверхзвуковых самолетов и баллистических ракет, а также при расчетах новых форм корпусов кораблей, формы лопаток газовых и водяных турбин и т. д.
Применяя законы гидромеханики и гидродинамики, в наши дни созданы совершенные по своим ходовым качествам скоростные суда на подводных крыльях, которые могут развивать скорость 80–90 км/час и выше. Это далеко не все примеры применения гидромеханики.
Развитие науки и техники всегда идет вместе, и эта органическая связь между ними как раз и обусловливает тот научный и технический прогресс и достижения, свидетелями которых мы сейчас являемся.
НОВЕЙШИЙ ЭТАП В РАЗВИТИИ ФИЗИКИ И ТЕХНИКИ
Современное развитие физики и техники характерно тем, что и в теоретической физике, и в технике за последние шестьдесят лет достигнуты значительные успехи в овладении силами природы и использовании их в интересах человека.
На службу человеку пришла атомная энергия; на повестку дня поставлен вопрос об использовании в мирных целях термоядерной энергии, запасы которой практически неисчерпаемы.
Создание теории относительности коренным образом изменило наши представления о пространстве и времени, продвинуло вперед исследования микромира, структуры атомов и атомных ядер, «элементарных» частиц материи и различных физических полей.
Успехи в области изучения электрических и магнитных явлений позволили совершить гигантский скачок в технике радиосвязи, передаче и обработке информации.
Освоение техники полупроводниковых приборов сделало возможным создание быстродействующих, малогабаритных и экономичных электронных вычислительных машин. Это позволило приступить к конструированию станков с программным управлением, различного рода самонастраивающихся систем, решать многие задачи, которые ранее не могли быть решены из-за необходимости проводить сложнейшие и громоздкие вычисления.
Читать дальше