Александр Виленкин - Мир множества миров. Физики в поисках иных вселенных

Он восхищался теорией Эйнштейна и погрузился в ее изучение со свойственным ему энтузиазмом. “Я неуч, – часто говорил он. – Я ничего не знаю. Я буду еще меньше спать и не позволю себе никаких отвлечений, поскольку вся эта так называемая жизнь – лишь бесполезная растрата времени”. [7] Цит. по: Э. А. Тропп, В. Я. Френкель, А. Д. Чернин. Александр Александрович Фридман. М.: “Наука”. – 1988. – с. 133. Он словно бы знал, что у него в запасе всего несколько лет, а сделать предстоит еще много.

В совершенстве освоив математику общей теории относительности, Фридман сконцентрировался на проблеме, которую считал центральной, – строении Вселенной в целом. Из статей Эйнштейна он знал, что без космологической постоянной теория не имеет статических решений, но хотел выяснить, какие варианты решений все же возможны. И тут был совершен радикальный шаг, обессмертивший его имя. Вслед за Эйнштейном Фридман предположил, что Вселенная однородна, изотропна и замкнута, то есть имеет геометрию трехмерной сферы. Но он отбросил статическую парадигму и позволил Вселенной двигаться. Радиус сферы и плотность вещества могли теперь изменяться во времени. Отказавшись от требования статичности, Фридман обнаружил, что уравнения Эйнштейна имеют решение. Они описывают сферическую вселенную, которая начинается с точки, расширяется до некоторого максимального размера, а потом вновь сжимается в точку. В начальный момент, который мы теперь называем Большим взрывом, все вещество Вселенной упаковано в единственную точку, в которой плотность вещества бесконечна. Она убывает, пока Вселенная расширяется, и растет, пока та сжимается обратно, чтобы опять стать бесконечной в момент “большого схлопывания”, когда Вселенная вновь становится точкой.

Большой взрыв и “большое схлопывание” отмечают начало и конец Вселенной. Из-за исчезающе малого размера и бесконечной плотности материи математические величины, фигурирующие в уравнениях Эйнштейна, становятся неопределенными, а пространство-время не может продолжаться за этими точками. Такие точки называют сингулярностями пространства-времени .

Двумерную сферическую вселенную можно представлять расширяющимся и сжимающимся воздушным шаром (рис. 3.1). Закорючки на его поверхности изображают галактики, и по мере расширения шара расстояния между ними будут расти. Таким образом, наблюдатель в любой галактике видит, что остальные галактики разбегаются. Расширение постепенно замедляется гравитацией и в конце концов останавливается, сменяясь сжатием. На фазе сжатия расстояния между галактиками будут убывать, и все наблюдатели увидят, что галактики приближаются к ним.

Не имеет большого смысла спрашивать, куда расширяется Вселенная. Мы изображаем вселенную воздушного шара расширяющейся в окружающее пространство, но это не имеет никакого значения для ее обитателей. Они привязаны к поверхности шара и не представляют себе третьего, радиального измерения. Подобным образом для наблюдателя в замкнутой вселенной трехмерное сферическое пространство – это все существующее пространство, и вне его ничего нет.

Вскоре после публикации этих результатов Фридман открыл другой класс решений с иной геометрией. Вместо искривления “на себя” пространство в этих решениях в определенном смысле искривляется “от себя”, что приводит к бесконечным (открытым) вселенным. Двумерным аналогом этого типа пространства является поверхность седла (рис. 3.2).

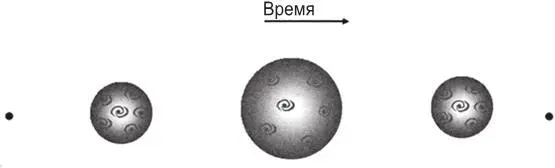
Рис. 3.1. Расширяющаяся и вновь сжимающаяся Вселенная.

И вновь Фридман обнаруживает, что расстояние, разделяющее любую пару галактик в открытой вселенной, растет, начиная с нулевого значения в сингулярности. Сначала расширение замедляется, но в данном случае гравитация недостаточно сильна, чтобы обратить его вспять, и со временем галактики приближаются к постоянной скорости удаления.

На границе между открытыми и закрытыми моделями находится вселенная с плоской, евклидовой геометрией. [8] Фридман не рассматривал случай плоской вселенной. Он был изучен Эйнштейном и де Ситтером в 1932 году. Она хоть и расширяется без ограничений, но делает это как будто на пределе, так что скорость расширения становится со временем все меньше и меньше.

Замечательная особенность решений Фридмана состоит в том, что они устанавливают простую связь между геометрией Вселенной и ее конечной судьбой. Если Вселенная замкнутая, она должна вновь сколлапсировать, а если открытая или плоская, то будет расширяться вечно. В своих статьях Фридман не отдавал предпочтения ни одной из моделей. [9] Простая связь между геометрией и судьбой Вселенной сохраняется, только если считать нулевой плотность энергии вакуума (космологическую постоянную). Подробнее об этом в главе 18.