Каниа Кан - Нейронные сети. Эволюция

Тогда целевое значение можно определить, как:

T = (А + ∆ А) х

Отобразим последнее соотношение на графике:

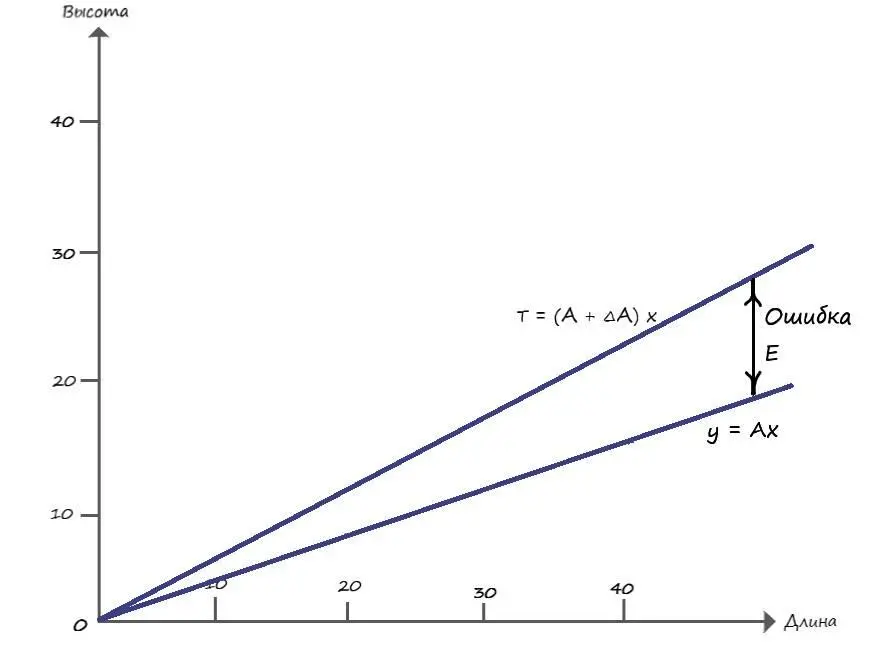
Подставим эти значения в формулу ошибки Е = T – у:

Е = T – у = (А + ∆А) х – Ах = Ax + (∆А) х – Ах = (∆А)х

Е = (∆А)х

Теперь зная, как ошибка Есвязана с ∆А, нетрудно выяснить что:

∆А = Е / х

Отлично! Теперь мы можем использовать ошибку Едля изменения наклона классифицирующей линии на величину ∆Ав нужную сторону.

Давайте сделаем это! При x = 40и коэффициенте А = 0,4, ошибка E = 5, попробуем найти величину ∆А:

∆А = Е/х = 5 / 40 = 0,125

Обновим наше начальное значение А:

А = А+ ∆А = 0,4 +0,125 = 0,525

Получается новое, улучшенное, значение коэффициента А = 0,525. Можно проверить это утверждение, найдя расчетное значение ус новыми параметрами:

y = А х = 0,525 * 40 = 21

В точку!

Теперь давайте узнаем на сколько надо изменить коэффициент А, чтоб найти верный ответ, для второй выборки из таблицы видов – жираф.

Целевые значения жирафа – высота y = 40, длина x = 20. Для того чтобы, разделительная линия не проходила через точку с параметрами жирафа, нам необходимо уменьшить целевое значение на единицу – y = 39.

Подставляем x = 20в линейную функцию, в которой теперь используется обновленное значение А=0,525:

у = Ax = 0,525 * 20 = 10,5

Значение – у = 10,5, далеко от значения y = 39.

Ну и давайте снова предпримем все те действия, что делали для нахождения параметров разделяющей линии в первом примере, только уже для второго значения из нашей таблицы.

Е = T – y = 39 – 10,5 = 28,5

Теперь параметр ∆Апримет следующее значение:

∆А = Е/х = 28,5 / 20 = 1,425

Обновим коэффициент крутизны А:

А = А+ ∆А = 0,525 +1,425 = 1,95

Получим обновленный ответ:

y = А х = 1,95 * 20 = 39

То есть, при x = 20, A = 1,95и ∆А = 1,425– функция возвращает в качестве ответа значение 39, которое и является желаемым целевым значением.

Представим все наши действия на графике:

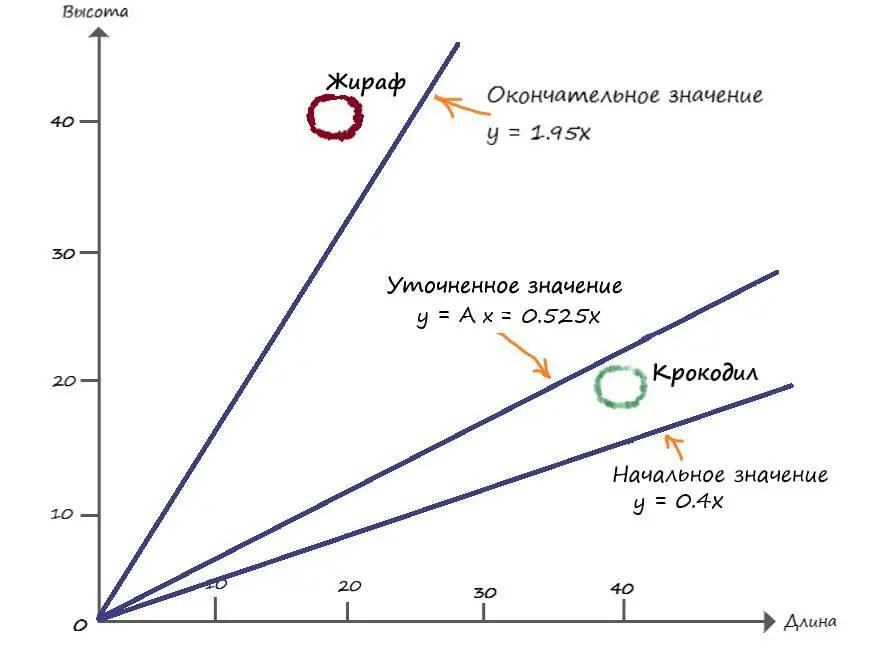
Теперь мы наблюдаем, что линия разделила два вида, исходя из табличных значений. Но полученная нами разделяющая линия лежит гораздо выше её воображаемого центра, к которому мы стремимся:

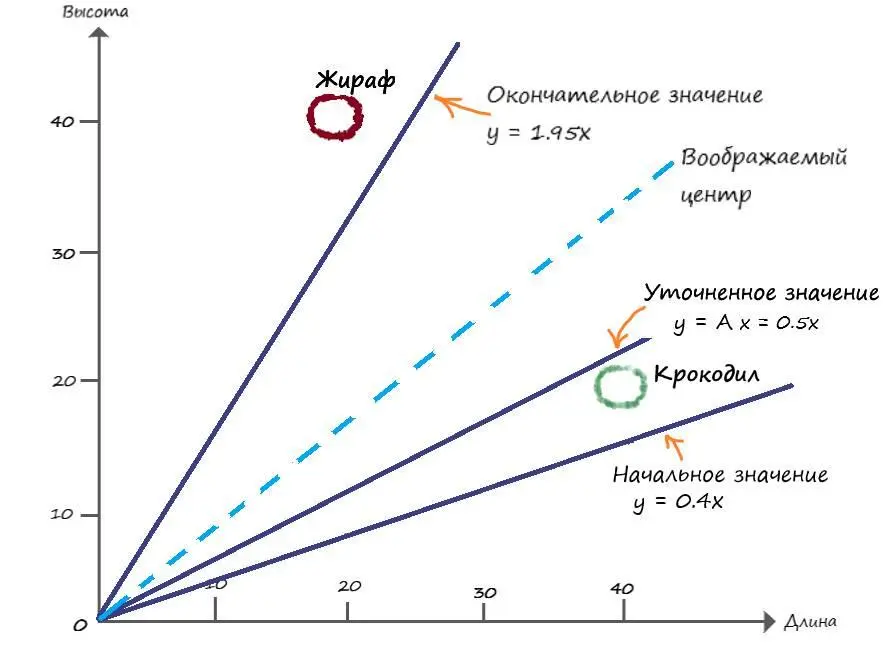
Но и это легко поправимо. Мы добьемся желаемого результата сглаживая обновления, через специальный коэффициент сглаживания – L, который часто называют как – скорость обучения.

Суть идеи: что каждый раз обновляя А, мы будем использовать лишь некоторую долю этого обновления. За счет чего, с каждым тренировочным примером, мы мелкими шагами будем двигаться в нужную нам сторону, и в конечном результате остановимся около воображаемой прямой по центру.

Давайте сделаем такой перерасчет:

∆А = L * (Е / X)

Выберем L =0,5в качестве начального приближения. То есть, мы будем использовать поправку вдвое меньшей величины, чем без сглаживания.

Повторим все расчеты, используя начальное значение А=0,4. Первый тренировочный пример дает нам у = Ax = О,4 * 40 = 16. При x = 40и коэффициенте А = 0,4, ошибка E = T – y = 21 – 16 = 5. Чтобы график прямой, не проходил через точку с нашими координатами, а проходил выше её, то принимаем целевое значение – T = 21.

Рассчитаем поправку: ∆А = L (Е / х) = 0,5*(5 / 40) = 0,0625. Обновленное значение: А = A + ∆А = 0,4 + 0,0625= 0,4625.

Сглаженное уточнение: y = Ax = 0,4625 * 40 = 18,5.

Теперь перейдем к расчетам следующего тренировочного примера.

Используя обновлённое на первом прогоне значение А, для второго тренировочного примера у = Ax = О,4625 * 20 = 9,25.

Значение, у = 9,25– всё так же далеки от значения y = 39, но мы все равно движемся в нужном направлении, но уже с меньшой скоростью.