Множество моделей как независимых случаев лжи
Теперь обратимся к моделям, которые помогают раскрыть преимущества многомодельного мышления. И представим в их контексте две теоремы: теорему Кондорсе о жюри присяжных и теорему о прогнозе разнообразия. Теорема Кондорсе о жюри присяжных основана на модели, созданной для объяснения преимуществ принципа большинства. В соответствии с ней присяжные принимают бинарное решение о виновности или невиновности подсудимого. Каждый присяжный в основном выносит правильное решение. Чтобы применить эту теорему к совокупности моделей, а не членов жюри присяжных, мы интерпретируем принятие решения каждым присяжным как классификацию согласно той или иной модели. В качестве классов могут выступать действия (купить или продать) или прогнозы (победителем станет представитель демократической или республиканской партии). Далее теорема указывает на то, что конструирование множества моделей и применение принципа большинства обеспечит более высокий уровень точности, чем при использовании одной из моделей данного множества. Модель опирается на концепцию состояния мира – полное описание всей значимой информации. Для жюри присяжных состояние мира складывается из доказательств, представленных в суде. Для моделей, которые оценивают социальный вклад благотворительного проекта, оно может представлять команду проекта, организационную структуру, план проведения мероприятий и особенности проблемы или ситуации, которую должен решить проект.
Теорема Кондорсе о жюри присяжных
Каждый из нечетного количества людей (моделей) классифицирует неизвестное состояние мира как истинное или ложное. Каждый человек (модель) классифицирует правильно с вероятностью 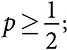 вероятность того, что другой человек (модель) выполнит правильную классификацию, статистически независима от правильности классификации любого другого человека (модели).
вероятность того, что другой человек (модель) выполнит правильную классификацию, статистически независима от правильности классификации любого другого человека (модели).
Теорема Кондорсе о жюри присяжных:большинство голосов обеспечивают правильную классификацию с более высокой вероятностью, чем любой отдельный человек (модель), а по мере увеличения количества членов жюри (моделей) точность решения, принятого большинством, приближается к 100 процентам [38].
Эколог Ричард Левинс объясняет, как применить логику этой теоремы к многомодельному подходу: «Мы пытаемся решить одну и ту же задачу с помощью ряда альтернативных моделей с разными упрощениями, но общим биологическим предположением. В таком случае, если эти модели, несмотря на различие исходных предположений, приводят к аналогичным результатам, мы имеем то, что можно назвать устойчивой теоремой, относительно свободной от деталей модели. Следовательно, истина находится на пересечении независимых случаев лжи» [39]. Обратите внимание, что здесь Левинс рассчитывает на единство классификации. Когда многие модели дают одну и ту же классификацию, наша уверенность должна повыситься.
Следующая теорема, о прогнозе разнообразия, применима к моделям, которые делают численные прогнозы или оценки. Она количественно оценивает влияние точности моделей и их разнообразия на точность их среднего [40] [41].
Теорема о прогнозе разнообразия
Погрешность множества моделей = средняя погрешность модели – разнообразие прогнозов моделей
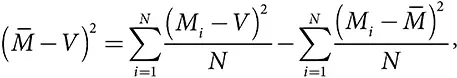
где M i – это прогноз i-й модели, 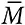 – среднее значений моделей, а V – истинное значение.
– среднее значений моделей, а V – истинное значение.
Теорема о прогнозе разнообразия описывает математическое тождество. Нам не нужно его проверять – оно всегда справедливо. Вот пример. Две модели прогнозируют количество «Оскаров», которые присудят одному из фильмов. Одна модель предсказывает два «Оскара», а другая – восемь. Среднее значение прогнозов двух моделей (прогноз на основе множества моделей) равно пяти. Если на самом деле фильм получит четыре «Оскара», то квадратичная погрешность прогноза первой модели будет равна 4 (2 в квадрате), второй – 16 (4 в квадрате), а множества моделей – 1. Разнообразие прогностических моделей составляет 9, поскольку прогноз каждой модели отличается от среднего прогноза на 3. В таком случае теорему о прогнозе разнообразия можно записать так: 1 (погрешность множества моделей) = 10 (средняя погрешность моделей) – 9 (разнообразие прогностических моделей).
Читать дальше

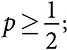 вероятность того, что другой человек (модель) выполнит правильную классификацию, статистически независима от правильности классификации любого другого человека (модели).
вероятность того, что другой человек (модель) выполнит правильную классификацию, статистически независима от правильности классификации любого другого человека (модели).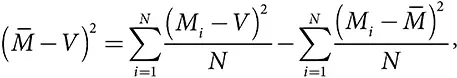
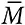 – среднее значений моделей, а V – истинное значение.
– среднее значений моделей, а V – истинное значение.










