Скотт Пейдж - Модельное мышление. Как анализировать сложные явления с помощью математических моделей

Этот парадокс объясняется тем, что у очень популярных людей больше друзей. На рис. 2.1 показана сеть дружеских связей в клубе карате, описанная Уэйном Закари. У человека, представленного черным кружком, шесть друзей, которые обозначены серыми кружками. У его друзей в среднем семь друзей, отмеченных белыми кружками. В целом в сети двадцать девять из тридцати четырех человек имеют друзей, которые пользуются большей популярностью, чем они сами [23]. Далее вы увидите, что если сделать ряд других допущений, то друзья большинства людей в среднем будут также более красивыми, добрыми, богатыми и умными, чем они сами.

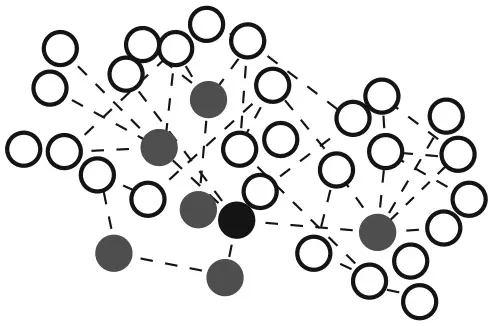
Рис. 2.1.Парадокс дружбы: у друзей человека больше друзей, чем у него самого

И последнее, самое важное: логика раскрывает обусловленность истины. Политик может утверждать, что снижение налогов увеличивает налоговые поступления в государственный бюджет, стимулируя экономический рост. Простейшая модель, в которой доход исчисляется как произведение налоговой ставки на уровень дохода, доказывает, что объем налоговых поступлений увеличивается только в случае, если процентный рост дохода превышает процентное сокращение налогов [24]. Следовательно, 10-процентное снижение подоходного налога увеличит объем налоговых поступлений только тогда, когда приведет к повышению уровня доходов более чем на 10 процентов. Логические рассуждения политика верны лишь при некоторых условиях, которые позволяют определить модели.

Сила обусловленности становится очевидной при сопоставлении утверждений, полученных с помощью моделей, и описательных утверждений, пусть и имеющих эмпирическое обоснование. Рассмотрим управленческую поговорку «в первую очередь самое важное» , смысл которой сводится к тому, что при наличии множества задач прежде всего нужно решать самую важную. Это правило также известно как «сначала крупные камни» , поскольку, складывая в ведро камни разных размеров, сначала вы должны уложить большие камни, потому что если первыми сложить мелкие камни, то крупные могут не поместиться.

Правило «сначала крупные камни» , выведенное на основе экспертных наблюдений, может быть верным в большинстве случаев, но оно не безусловно. Подход, основанный на применении моделей, вывел бы оптимальное правило, исходя из конкретных предположений о задаче. В задаче об упаковке в контейнеры множество предметов разных размеров (или с разным весом) необходимо уложить в контейнеры определенного объема, использовав при этом как можно меньше контейнеров. Представьте, что вы упаковываете вещи из своей квартиры и складываете их в коробки размером примерно 60×60 сантиметров. Упорядочить вещи по размеру и положить каждую из них в первую коробку с достаточным объемом (метод, известный как алгоритм первого подходящего ) – весьма эффективный подход. И правило «сначала крупные камни» здесь вполне применимо. Однако предположим, что мы рассматриваем более сложную задачу: выделить место на Международной космической станции для исследовательских проектов. У каждого проекта есть вес полезного груза, размер и требования к системе электропитания наряду с требованиями ко времени и когнитивным способностям астронавтов. Кроме того, каждый исследовательский проект вносит определенный научный вклад. Даже если бы мы установили какой-либо показатель значимости как взвешенное среднее всех этих характеристик, правило «сначала крупные камни» не сработало бы, учитывая размерность взаимозависимостей. В данном случае гораздо лучше работали бы более сложные алгоритмы и, возможно, рыночные механизмы [25]. Таким образом, при одних условиях правило «сначала крупные камни» эффективно, тогда как при других нет. Применение моделей позволяет выяснить, когда целесообразно сначала складывать крупные камни, а когда нет.

Критики формального подхода заявляют, что модели просто переформатируют то, что нам уже известно, что они наливают старое вино в сверкающие математические бутылки, что нам не нужна модель для понимания того, что две головы лучше одной и что промедление смерти подобно. Мы можем осознать ценность самоотверженности, прочитав историю о том, как Одиссей привязал себя к мачте корабля. Такая критика не признает того факта, что выводы, сделанные с помощью моделей, принимают условную форму: если условие A выполняется, то наступает следствие B (например, если вы складываете что-то в контейнеры и размер – единственное ограничение, укладывайте сначала самые крупные предметы). Уроки, почерпнутые из литературы, или общеизвестные советы великих мыслителей во многих случаях не содержат никаких условий. Пытаясь жить или управлять другими людьми согласно безусловным правилам, мы потеряемся в море противоположных поговорок. Действительно ли две головы лучше одной? Или у семи нянек дитя без глазу?