Мелани Митчелл - Идиот или гений? Как работает и на что способен искусственный интеллект

Розенблатт изобрел перцептрон, обратив внимание на то, как нейроны обрабатывают информацию. Нейрон – это клетка мозга, которая получает электрический или химический импульс от связанных с нею нейронов. Грубо говоря, нейрон суммирует все импульсы, которые получает от других нейронов, и сам посылает импульс, если итоговая сумма превышает определенный порог. Важно, что разные связи ( синапсы ) конкретного нейрона с другими нейронами имеют разную силу, а потому, суммируя импульсы, нейрон придает больше веса импульсам от сильных связей, чем импульсам от слабых связей. Нейробиологи полагают, что поправки на силу связей между нейронами – важнейший элемент процесса обучения, происходящего в мозге.

С точки зрения специалиста по информатике (или, как в случае с Розенблаттом, психолога), обработку информации нейронами можно смоделировать в компьютерной программе – перцептроне, – которая преобразует много численных входных сигналов в один выходной сигнал. Аналогия между нейроном и перцептроном показана на рис. 1. На рис. 1A мы видим нейрон с ветвистыми дендритами (волокнами, которые проводят входящие импульсы в клетку), телом клетки и аксоном (или выводным каналом). На рис. 1B изображен простой перцептрон. Как и нейрон, перцептрон суммирует все входящие сигналы. Если итоговая сумма равняется порогу перцептрона или превышает его, перцептрон выдает значение 1 (“передает сигнал”); в противном случае он выдает значение 0 (“не передает сигнал”). Чтобы смоделировать различную силу связей нейрона, Розенблатт предложил присваивать каждому входному сигналу перцептрона численный вес и умножать входной сигнал на его вес, прежде чем прибавлять к сумме. Порог перцептрона – это число, определяемое программистом (или, как мы увидим, узнаваемое самим перцептроном).

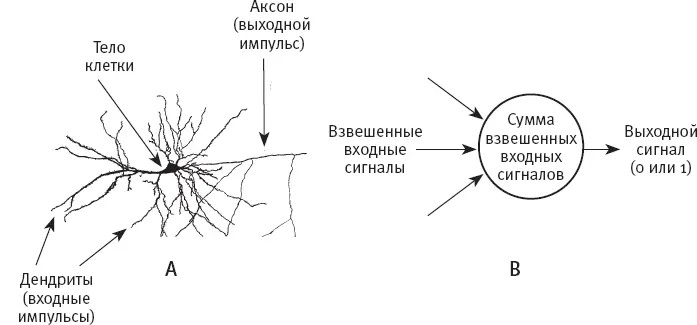
Рис. 1. A: нейрон в мозге; В: простой перцептон

Иными словами, перцептрон – это простая программа, которая принимает решение “да или нет” (1 или 0) в зависимости от того, достигает ли сумма взвешенных входных сигналов порогового значения. Вероятно, вы тоже время от времени принимаете такие решения в жизни. Например, вы узнаете мнение нескольких друзей о конкретном фильме, но вкусам одних друзей доверяете больше, чем вкусам других. Если сумма “дружеских восторгов” – при большем весе мнений тех друзей, которым вы доверяете больше, – достаточно высока (то есть превышает некоторый неосознанный порог), вы решаете посмотреть фильм. Именно так перцептрон выбирал бы фильмы к просмотру, если бы у него были друзья.

Вдохновленный сетями нейронов в мозге, Розенблатт предположил, что сети перцептронов могут выполнять визуальные задачи, например справляться с распознаванием объектов и лиц. Чтобы понять, как это может работать, давайте изучим, как с помощью перцептрона решить конкретную визуальную задачу: распознать рукописные цифры вроде тех, что показаны на рис. 2.

Давайте сделаем перцептрон детектором восьмерок – в таком случае он будет выдавать единицу, если входным сигналом служит изображение цифры 8, и ноль, если на входном изображении будет любая другая цифра. Чтобы создать такой детектор, нам нужно (1) понять, как превратить изображение в набор численных входных сигналов, и (2) определить численные значения весов и порог перцептрона для формирования верного выходного сигнала (1 для восьмерок и 0 для других цифр). Я рассмотрю эту задачу более подробно, поскольку многие из этих принципов понадобятся нам при обсуждении нейронных сетей и их применения в компьютерном зрении.

Рис. 2. Примеры рукописных цифр

На рис. 3A показана увеличенная рукописная восьмерка. Каждый квадрат координатной сетки – это пиксель с численным значением “насыщенности”: насыщенность белых квадратов равняется 0, насыщенность черных – 1, а насыщенность серых имеет промежуточное значение. Допустим, все изображения, которые мы даем перцептрону, подогнаны к единому размеру – 18 × 18 пикселей. На рис. 3B показан перцептрон для распознавания восьмерок. У этого перцептрона 324 (то есть 18 × 18) входных сигнала, каждый из которых соответствует одному пикселю из сетки 18 ×18. При получении изображения, подобного показанному на рисунке 3A, каждый входной сигнал настраивается на насыщенность соответствующего пикселя. Каждому входному сигналу также присваивается свой вес (на рисунке не показан).