Александр Боксер - Астрология и рождение науки. Схема небес

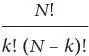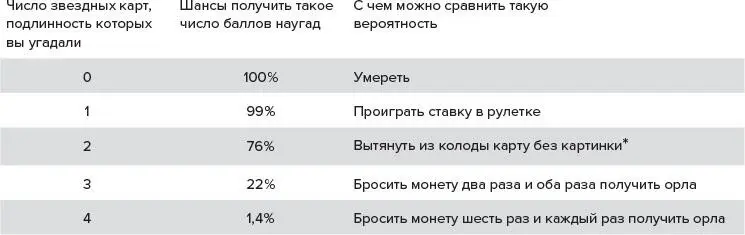
Таблица 1.1. Баллы за сортировку звездных карт

* Имеется в виду туз, двойка, …, десятка, а не валет, дама или король. – Прим. перев.

Нередко высокая или низкая вероятность некоторого события противоречит нашей интуиции. Вам казалось, что угадать три подлинные карты созвездий – это нечто? Как указано в таблице 1.1, это не более удивительно, чем бросить монету два раза и оба раза получить орла, – другими словами, ничего особенного.

Угадайка наподобие той, что представлена на рис. 1.2, бывает весьма полезна, когда нет других способов получить информацию, например, о том, правда ли человек так искусен в опознании созвездий, как утверждает. Собственно, это пример так называемого статистического теста – тщательно продуманного эксперимента, в котором знание законов вероятностей помогает извлечь из фактов обоснованный ответ на поставленный вопрос. На самом деле я составил рис. 1.2 как точное подобие одного из самых знаменитых тестов в истории статистики, так называемого чайного эксперимента. Его формат был разработан Рональдом Фишером, одним из титанов статистики XX века, когда одна из его коллег заявила, будто может отличить, что было сначала налито в ее чашку: чай или молоко. (Предание гласит, что она легко рассортировала восемь чашек чая с молоком, расставленные в случайном порядке, на правильные группы по четыре чашки, и Фишеру пришлось нехотя признать ее талант чайного дегустатора.) [12] См.: Ronald A. Fisher. The Design of Experiments. Edinburgh; London: Oliver and Boyd, 1935. Ch. 2. Без математики та же история (включая утверждение о правильной сортировке всех восьми чашек чая) рассказана здесь: David Salsburg. The Lady Tasting Tea: How Statistics Revolutionized Science in the Twentieth Century. New York: W. H. Freeman, 2001. Ch. 1.

В наше время статистические тесты широко применяются в науке и промышленности, от оценки эффективности лечения до оценки влияния дизайна веб-страницы на число пользовательских кликов и даже для оценки постоянства вкуса пива от бутылки к бутылке. Такие тесты применимы к числовым данным любого рода, и для их планирования не требуется знать контекст – ведь эти тесты имеют дело с голыми числами и выдают в качестве результата голые числа. Поэтому они так полезны в самых разных областях исследований, включая такие ненадежные и быстро меняющиеся сферы, как гуманитарные и социальные тренды, где у ученых нет надежных теорий. В таких случаях статистические тесты – это единственное, на что можно положиться, чтобы как-то судить о положении вещей.

У такого подхода, где выводы делаются только по голым числам, без опоры на соображения за пределами статистики, есть коварный недостаток: оказывается, слишком легко ошибиться в оценке значения редкого результата. Трудно сопротивляться искушению придать глубокий смысл маловероятному событию, объявить, что случилось большее, чем простое совпадение. Особенно когда случай подтверждает теорию, в которую нам ужасно хочется верить. Но что именно считать редким , вопрос относительный. Если процедура повторяется многократно, редкие результаты появляются практически с неизбежностью, и они будут сбивать нас с толку, если мы не ведем учет тех случаев, где ничего редкого не произошло [13] Во многих областях исследований порогом статистической значимости для публикации открытия считается достоверность 5 %, или 1 из 20. Каждое двадцатое из таких открытий должно быть случайным шумом, а не эффектом, о котором заявляют авторы. См., например: John P. A. Ioannides. Why Most Published Research Findings are False // PLoS Med. 2005. e124. Ситуация еще хуже, если исследователи повторяют эксперимент, пока не добьются «значимого» результата. В физике элементарных частиц за пороговую значимость принимается пять сигм, это примерно 1 на 3,5 миллиона. Если бы мы открыли 3,5 миллиона фундаментальных физических частиц (чего на самом деле не было), следовало бы подозревать, что примерно одно из открытий при дальнейших исследованиях окажется результатом случайной флуктуации. .

Возвращаясь к примеру со звездными картами, заметим, что существует ровно 70 способов отобрать четыре из восьми картинок. На этот случай есть известная математическая формула: если вы создаете группу, содержащую k предметов, имея в своем распоряжении N кандидатов (так называемый выбор из N по k ), то число вариантов составляет

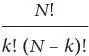
(Здесь восклицательный знак означает вычисление факториала. Например, 4! читается как «четыре факториал» и означает 4×3×2×1 = 24.)