Светлана Криворучко - Состояние, тенденции и перспективы развития наличного денежного обращения в России

В связи с гетероскедастичностью остатков (разницы между фактом и прогнозом, сделанным по данному уравнению) решение придется осуществлять обобщенным МНК, который, в отличие от обычного МНК, применяется к данным, преобразованным следующим образом:

Данное преобразование позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии.

В результате мы получили в логарифмическом виде следующее уравнение регрессии:

LOG(GDP_US)= 5,996 + 0,474*LOG(M1_US). (Б.4)

Все коэффициенты уравнения у нас получились статистически значимыми с 0,05 уровнем надежности, а коэффициент детерминации R-squared оказался равен 0,864, то есть изменения независимой переменной M1_US в 86,4 % случаев объясняют динамику зависимой переменной GDP_US.

После потенцирования получаем следующее степенное уравнение регрессии:

GDP_US= 401,77*M1_US 0,474(Б.5)

Последнее уравнение можно интерпретировать следующим образом: в период с 2002 г. по 2012 г. рост объема денежного агрегата М1 на 1,0 % приводил к росту объема ВВП США на 0,474 % (коэффициент эластичности) при исходном уровне (его трактуют как гипотетическую величину ВВП, независимую от М1), равном 401,77 млрд долл.

Вычисление коэффициента эластичности между ростом объема денежного агрегата М2 и ростом ВВП: для того, чтобы найти степенное уравнение регрессии между зависимой переменной «ВВП США, в текущих ценах, млрд долл.» и независимой переменной «денежный агрегат M2 США, в млрд долл.», обозначим их символами, соответственно, как GDP_US и M2_US, а затем прологарифмируем и решим линеаризованное уравнение регрессии с помощью статистической программы EViews. Подробный вывод данных по решению данного уравнения регрессии представлен в таблице Б.3 Приложения Б.

В результате мы получили в логарифмическом виде следующее уравнение регрессии:

LOG(GDP_US)= 3,962 + 0,619*LOG(M2_US). (Б.6)

Все коэффициенты уравнения у нас получились статистически значимыми с 0,05 уровнем надежности, а коэффициент детерминации R-squared оказался равен 0,910, то есть изменения независимой переменной M2_US в 91,0 % случаев объясняют динамику зависимой переменной GDP_US.

После потенцирования получаем следующее степенное уравнение регрессии:

GDP_US= 52,58*M2_US 0’ 619(Б.7)

Последнее уравнение можно интерпретировать следующим образом: в период с 2002 г. по 2012 г. рост объема денежного агрегата М2 на 1,0 % приводил к росту ВВП с США на 0,619 % (коэффициент эластичности) при исходном уровне (его трактуют как гипотетическую величину ВВП, независимую от М2), равном 52,58 млрд долл.

Таблица Б.1 – Решение степенного уравнения регрессии, показывающего зависимость роста ВВП США от роста объема денежного агрегата М0

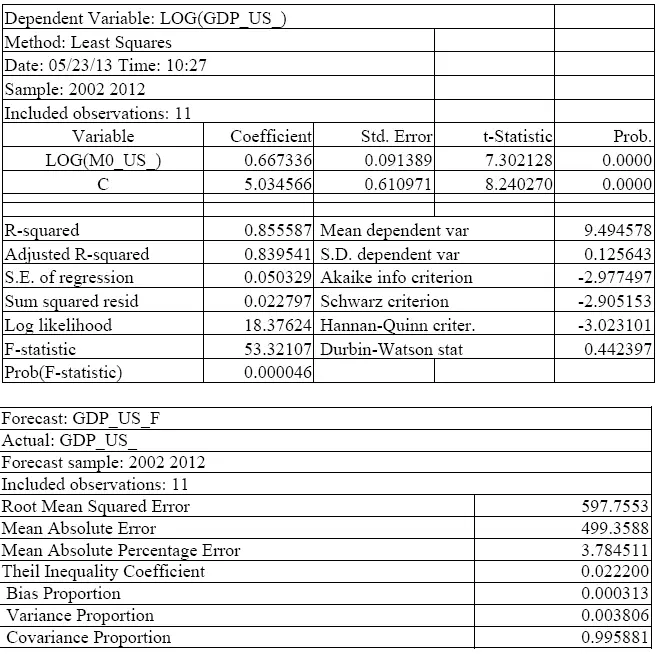
Источник: составлено автором

Таблица Б.2 – Решение степенного уравнения регрессии, показывающего зависимость роста ВВП США от роста объема денежного агрегата М1

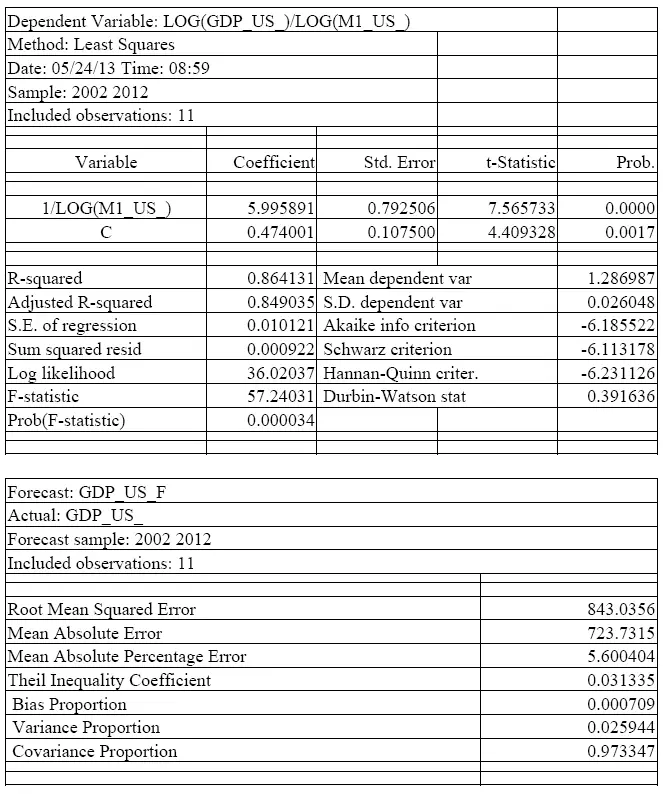
Источник: составлено автором

Таблица Б.3 – Решение степенного уравнения регрессии, показывающего зависимость роста ВВП США от роста объема денежного агрегата М2

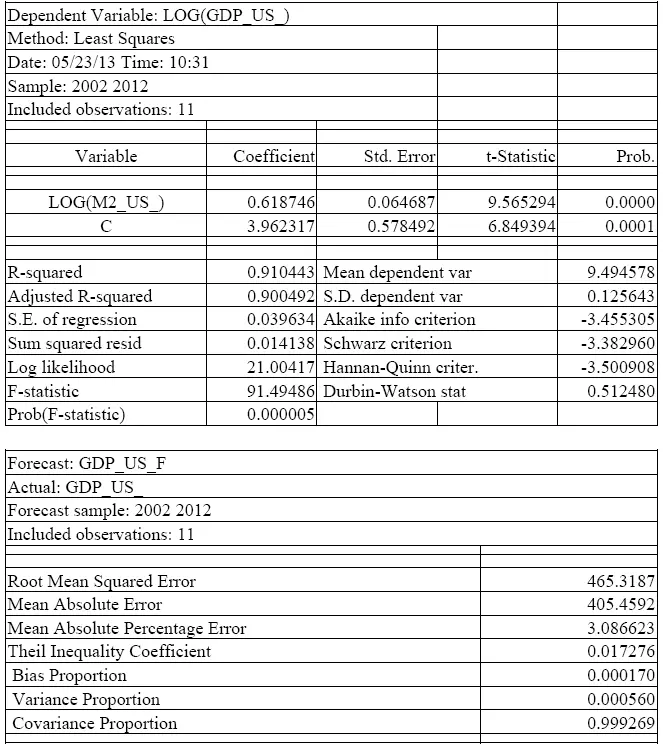
Источник: составлено автором

(обязательное)

Алгоритм вычисления коэффициента эластичности между ростом объема различных денежных агрегатов и ростом ВВП в ФРГ

Вычисление коэффициента эластичности между ростом объема денежного агрегата М1 и ростом ВВП: для того, чтобы найти степенное уравнение регрессии между зависимой переменной «ВВП ФРГ, в текущих ценах, млрд евро» и независимой переменной «денежный агрегат M1 ФРГ, в млрд евро», обозначим их символами, соответственно, как GDP_GE и M1_GE, а затем прологарифмируем и решим линеаризованное уравнение регрессии с помощью статистической программы EViews. В связи с гетероскедастичностью остатков решение придется выполнить обобщенным МНК. Подробный вывод данных по решению данного уравнения регрессии представлен в таблице В.1 Приложения В.

В результате мы получили в логарифмическом виде следующее уравнение регрессии:

LOG(GDP_GE)= 6,132+0,243*LOG(M1_GE). (В.1)