Александр Петров - Гравитация. От хрустальных сфер до кротовых нор

Нулевая частота означает, что нет никакого сигнала вообще! Из-под сферы радиуса r g световые сигналы не выходят, гравитационные силы не дают им вырваться во внешнюю окрестность. То есть, действительно, это сфера, где вторая космическая скорость становится равной скорости света. Поэтому из-под сферы радиуса r g невозможно распространение наружу никакой формы материи. Таким образом, эта сфера оказывается барьером, за который внешний наблюдатель не в состоянии заглянуть. Именно поэтому она получила удачное название горизонта событий , а сам объект стали называть черной дырой .

Термин черная дыра подсказал известному американскому физику-теоретику Джону Уилеру (1911–2008) один из студентов на конференции в 1967 году. Но еще ранее, в 1964 году, его использовала Анна Ивинг в докладе на собрании Американской ассоциации содействия науке.

До сих пор мы рассматривали фиксированные точки пространства и наблюдателей, связанных с ними. Теперь давайте проследим за свободно падающим телом. Пусть падение начинается из состояния покоя из удаленной области, где почти нет искривления, откуда мы будем отслеживать его траекторию. В восприятии удаленного наблюдателя история падения будет следующей. Сначала движение не будет вызывать удивления. Скорость будет нарастать медленно, затем все быстрее и быстрее, вполне соответствуя закону всемирного тяготения. Затем, на расстояниях от центра, сравнимых с гравитационным радиусом, нарастание скорости падения станет катастрофическим. Здесь мы тоже не очень удивимся, мы объясним это тем, что из зоны соответствия с гравитацией Ньютона объект попал в зону сильных искривлений. А на расстояниях долей гравитационного радиуса от горизонта событий он, к нашему изумлению, начнет резко тормозить и все медленней приближаться к горизонту событий, а в результате, никогда его не достигнет. Но здесь тоже нечего удивляться, недавно мы установили, что для удаленного наблюдателя все процессы при приближении к горизонту событий замирают, падение тела – не исключение.

Эффект того, что из-под горизонта событий ничего не выходит наружу, мы объяснили наличием чрезвычайно сильного гравитационного воздействия. Этот ответ, конечно, правильный, поскольку ничего, кроме гравитации, не рассматривается. Однако он не конструктивный, так как не позволяет понять механизм тех явлений, о которых мы только что говорили. Нет никакого представления о том, что происходит под горизонтом, и происходит ли вообще что-то. С другой стороны, мы договорились, что в эйнштейновской теории гравитационных сил, как таковых, нет вообще. Есть искривление пространства-времени. Поэтому, давайте, шаг за шагом перейдем к описанию в рамках геометрической теории.

Мы уже убедились, что в СТО использование светового конуса помогает понять многие явления. В ОТО, в искривленном пространстве-времени, имеет больший смысл представлять его не на всей диаграмме, а в окрестности каждой мировой точки. Это будет локальный световой конус, образованный касательными к световым геодезическим в данной точке. Уравнение светового конуса имеет простой вид – интервал приравнивается нулю: ds = 0.

На рис. 8.2 схематически изображены световые конусы для геометрии Шварцшильда. Предполагая, что движения происходят по радиальным направлениям, диаграмма представлена в координатах r и t . Эти координаты для удаленного наблюдателя в его собственной системе отсчета определяют истинные расстояние и время. Поэтому картина физических явлений, представленная с помощью r и t, – это как раз та картина, которую будет воспринимать удаленный наблюдатель. На рисунке видно, что на значительном удалении «лепестки» конуса расположены под углом 45°, то есть так, как в плоском пространстве-времени. Вертикальные линии соответствуют тем самым зафиксированным (неподвижным) наблюдателям, о которых мы говорили недавно. По мере приближения к черной дыре конус становится все уже, на горизонте он «слипается» и превращается в одну вертикальную линию. Вертикальная линия для удаленного наблюдателя означает, что свет «остановился», его скорость стала «нулевой». Это и означает, что на горизонте все явления замораживаются. Расчет нулевой геодезической показывает, что для удаленного наблюдателя свет никогда не достигнет горизонта.

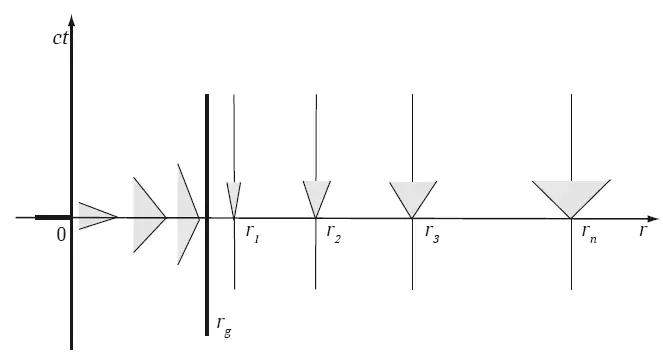
Рис. 8.2. Пространство-время геометрии Шварцшильда в координатах удаленного наблюдателя