s 2= c 2 t′ 2– x′ 2– y′ 2– z′ 2= c 2 t′ 2– r′ 2.
то есть s = s’ .
В инвариантности интервала нет ничего удивительного – это лишь геометрическое свойство пространства Минковского, а не следствие каких-то принципов. Действительно, поскольку интервал – это длина в метрическом пространстве, то эта величина не зависит от способов измерения (использования той или иной координатной сетки). Замечательно другое – известные геометрические свойства псевдоевклидовых пространств оказались весьма полезными для описания СТО.
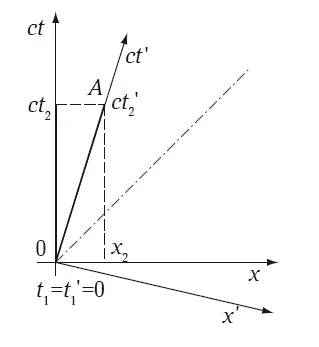
Рис. 5.3. Переход к другой инерциальной системе на диаграмме пространства Минковского
Эффекты сокращения длины, замедления времени, сложение скоростей в СТО являются следствием лоренц-инвариантности. Остановимся на первых двух. Рассмотрим линейку, собственная длина которой l 0– это длина в ее системе покоя. Пусть система покоя для выбранной линейка – это система K’ , которая движется относительно нас (системы K) со скоростью V . Тогда, если концы линейки имеют координаты
x 1 ′ и x 2 ′ , то l 0= x 2 ′ – x 1 ′ .
Определим длину этого отрезка с точки зрения наблюдателя системы K . Для этого нужно в один и тот же (!) момент времени t определить координаты концов линейки x 2и x 1в системе K . Тогда для нас длина линейки буде иметь величину l = x 2– x 1. Чтобы определить каждое из значений x 2и x 1через соответствующие штрихованные координаты используем первую часть преобразований Лоренца (Б) каждый раз с одним и тем же значением t. Затем составим разницу и получим 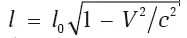 , то есть для нас (покоящейся системы K ) движущаяся линейка становится короче.
, то есть для нас (покоящейся системы K ) движущаяся линейка становится короче.
Подтвердим вывод о замедлении времени. Находясь в системе K, будем отслеживать ход часов в системе K′ , которые находятся в точке x′. Для нас часы в системе K идут одинаково во всех точках, поэтому часы системы K′ можно сравнивать с любыми нашими. Не теряя общности, можно предположить, что x′ = 0 и моменты первого сравнения в обеих системах также нулевые: t 1 ′ = t 1= 0. Вопрос в том, как начнут разниться показания в любой следующий момент сравнения t 2(а для системы K′ – t 2 ′ ). Теперь удобнее использовать вторую часть преобразований Лоренца (А). Получаем 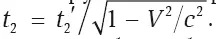 . Как видно, показания часов в нашей системе K будут больше, чем в K′ , хотя в обоих случаях отсчет начинался с нуля. Таким образом, движущиеся часы идут медленнее.
. Как видно, показания часов в нашей системе K будут больше, чем в K′ , хотя в обоих случаях отсчет начинался с нуля. Таким образом, движущиеся часы идут медленнее.
На этом этапе важно сделать замечание. Мы все больше убеждаемся, что пространство и время физически объединены в единое целое – пространственно-временной континуум. Действительно, и пространственные, и временные координаты участвуют в единых преобразованиях; инвариантная величина интервал построена как из временных промежутков, так и из пространственных отрезков. Несмотря на это, и пространство, и время сохраняют свою физическую сущность – протяженность и длительность. Формально это различие состоит в том, что временная часть входит в интервал со знаком « плюс », а пространственная – со знаком « минус ».
Мы уже отметили, что квадраты интервалов могут быть положительными, нулевыми и даже отрицательными. Для положительных – временная часть превосходит пространственную, и они называются времениподобными. Нулевые соответствуют распространению света и называются светоподобными ; совокупность светоподобных, представляющая распространение световых лучей из какой-либо мировой точки, образует, так называемый, световой конус в пространстве Минковского. На рис. 5.4 такой световой конус относится к началу координат и делит пространство-время на две части: внутри и вне конуса. Наконец, для отрицательных квадратов интервалов, пространственная часть превышает временную, и они называются пространственноподобными.
Для нас более интересны времениподобные интервалы. Почему? Отрезок прямой 0 A , соединяющий мировую точку внутри конуса и начало координат на рис 5.4 вполне можно интерпретировать как путь материальной частицы , движущейся прямолинейно и равномерно. Скорость ее меньше скорости света, и поэтому путь находится внутри конуса. Квадрат интервала между точкой А и началом координат s 2= c 2 t 2– xА 2 – положительный, и это относится ко всем мировым точкам внутри конуса, скажем A′. Наклон соответствующих отрезков пути меньше , чем у светового конуса. Если бы мы попытались интерпретировать отрезки пути с наклоном больше , чем у светового конуса, как путь материальной частицы, то нужно было бы говорить о скоростях больших скорости света. Но для материальной частицы это невозможно, мы об этом еще скажем.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


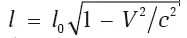 , то есть для нас (покоящейся системы K ) движущаяся линейка становится короче.
, то есть для нас (покоящейся системы K ) движущаяся линейка становится короче.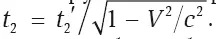 . Как видно, показания часов в нашей системе K будут больше, чем в K′ , хотя в обоих случаях отсчет начинался с нуля. Таким образом, движущиеся часы идут медленнее.
. Как видно, показания часов в нашей системе K будут больше, чем в K′ , хотя в обоих случаях отсчет начинался с нуля. Таким образом, движущиеся часы идут медленнее.









