Сергей Попов - Все формулы мира

В 1921 г. немецкий математик Теодор Калуца представил модель, объединяющую гравитацию и электромагнетизм в пятимерном пространстве Минковского. В рамках этого подхода из уравнений общей теории относительности удалось получить классические уравнения Максвелла.

Первые серьезные теоретические модели в этой области появились в 1930-е гг., когда Энрико Ферми начал работать над описанием бета-распада.

Детальнее об орбитальном хаосе можно прочесть в 8-й главе книги Иэна Стюарта «Величайшие математические задачи» (М.: Альпина нон-фикшн, 2019).

В апреле 2019 г. были представлены изображения центральной части галактики М87, полученные с помощью Телескопа горизонта событий. Удалось рассмотреть линзированное изображение фотонной сферы центральной сверхмассивной черной дыры. Наблюдать черную дыру в нашей Галактике с помощью этой системы телескопов гораздо сложнее, так как наша черная дыра примерно в тысячу раз менее массивна, а значит, во столько же раз меньше ее размер. Из-за этого переменность данного объекта гораздо более быстрая, что не позволяет получить четкую картинку при длительных наблюдениях на Телескопе горизонта событий, продолжающихся несколько часов. Возможно, радикальным выходом является лишь создание системы космических телескопов, работающих как интерферометр в миллиметровом диапазоне длин волн.

Благодаря работе К. Финкельштейна, написанной в 1958 г., возникло современное понимание свойств горизонта черной дыры.

«Дыр бул щыл» и «убеш щур скум» – цитаты из стихотворения А. Крученых. Пример так называемого заумного языка.

Тензор – математический объект. Тензоры удобно представлять как многомерные таблицы (матрицы). Это отличает их от более привычных скалярных величин (одно число) и векторов (одномерный массив чисел), хотя можно рассматривать векторы и скаляры как частные случаи тензоров.

Например, такие числа, как седенионы, пока не нашли широкого применения в физике. Однако теоретики пытаются приспособить их для работы над квантовой гравитацией и теорией великого объединения. Младшие братья седенионов, октонионы, тоже пока не слишком востребованы физиками.

Гипотетический одноклеточный организм LUCA (Last Universal Common Ancestor, или последний универсальный общий предок). Популяция таких организмов представляет собой последних по времени общих предков всех современных живых организмов на Земле. Гипотеза об их существовании была впервые высказана Чарлзом Дарвином. С тех пор генетические исследования позволили получить множество аргументов в ее пользу.

Кеплер в основном пользовался данными наблюдений Марса, полученными Тихо Браге – лучшим астрономом-наблюдателем того времени, а может быть, и всей дотелескопической эпохи.

Большая полуось – это, по сути, половина длинного диаметра эллипса, который проходит через центр и оба фокуса эллипса.

Уже во времена Лапласа возникла проблема объяснения движения Юпитера и Сатурна, которые из-за взаимного влияния заметно отклоняются от идеальных кеплеровских эллипсов.

Это так называемый принцип соответствия: новая научная теориядолжна включать старую и ее результаты как частный (предельный) случай. Большую популярность принцип приобрел благодаря Нильсу Бору после появления квантовой механики.

Потенциал Пачинского – Вииты был предложен в 1980 г. Он применяется при приближенных расчетах движения тел на расстоянии больше нескольких шварцшильдовских радиусов от массивного компактного тела. В формуле для гравитационного потенциала в знаменателе расстояние r , отсчитываемое от центра массивного тела, заменено на разность этого расстояния и радиуса Шварцшильда:

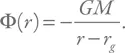
Разумеется, макроскопические параметры объектов могут определяться квантовыми законами. Например, массы и радиусы нейтронных звезд и белых карликов зависят от квантовых процессов, происходящих на микроуровне. Наблюдая в лабораторных экспериментах сверхпроводимость и сверхтекучесть, мы также сталкиваемся с макроскопическим проявлением квантовых свойств вещества.

Вопросы происхождения жизни рассматриваются, например, в книге М.А. Никитина «Происхождение жизни. От туманности до клетки» (М.: Альпина нон-фикшн, 2019).