Чарльз Петцольд - Код. Тайный язык информатики

Наиболее интересными явлениями в мире UNIX в последние годы стали Фонд свободного программного обеспечения (Free Software Foundation, FSF) и проект GNU, основанные Ричардом Столлманом. Аббревиатура GNU является акронимом выражения GNU’s Not UNIX («GNU не UNIX»), что, разумеется, правда. Вместо этого программы, разработанные в рамках проекта GNU, являются совместимыми с операционной системой UNIX, однако распространяются так, что не могут стать чьей-либо собственностью. Благодаря проекту GNU появилось множество UNIX-совместимых служебных программ и инструментов, а также Linux — ядро операционной системы, совместимой с UNIX. Главный создатель ставшего в последние годы популярным ядра Linux — Линус Торвальдс, американский программист из Финляндии.

Однако главная тенденция в развитии ОС, зародившаяся в середине 1980-х, — это разработка таких крупных и сложных систем, как Apple Macintosh и Microsoft Windows, где графические пользовательские интерфейсы и широкие возможности видеосистем применяются для упрощения работы с приложениями. Эту тенденцию я опишу в главе 25.

В повседневной жизни мы легко оперируем целыми числами, дробями и процентами одновременно. Мы покупаем полдесятка яиц, заплатив налог в размере 8¼ процента из денег, полученных за 2¾ часа сверхурочной работы, оплаченной по тарифу, в полтора раза превышающему обычный. Большинство людей не испытывают трудностей при использовании таких величин. Услышав от статистиков о том, что «среднее американское домохозяйство состоит из 2,6 человека», мы не ужасаемся при мысли о связанных с этим повсеместных увечьях.

Тем не менее когда дело касается компьютерной памяти, переключение между целыми и дробными числами оказывается сложнее. Да, все данные хранятся в компьютерах в виде битов, то есть в виде двоичных чисел. Однако одни виды чисел выразить в битах гораздо легче, чем другие.

Сначала мы использовали биты для представления положительных целых или положительных натуральных чисел. Мы также узнали, как с помощью дополнения до двух можно отобразить отрицательные целые числа, чтобы упростить операцию сложения. В следующей таблице показано, какие диапазоны положительных и отрицательных целых чисел (отрицательные числа выражены с помощью дополнения до двух) можно хранить в ячейках памяти емкостью 8, 16 и 32 бит.

Число битов

Диапазон целых положительных чисел

Диапазон целых отрицательных чисел

8

От 0 до 255

От –128 до 127

16

От 0 до 65 535

От –32 768 до 32 767

32

От 0 до 4 294 967 295

От –2 147 483 648 до 2 147 483 647

Однако на этом мы и остановились. Помимо целых чисел математики также различают рациональные числа, которые могут быть представлены в качестве отношения двух целых чисел. Это отношение также называется дробью . Например, дробь ¾ — рациональное число, отношение чисел 3 и 4. Это число также можно записать в виде десятичной дроби : 0,75. Десятичная дробь остается отношением двух чисел, в данном случае 75/100.

В главе 7 рассказывалось, что в десятичной системе счисления цифры слева от десятичного разделителя являются множителями целых положительных степеней числа 10, а цифры справа — множителями целых отрицательных степеней числа 10. В одном из примеров я показал, что число 42 705,684 равно:

4 × 10 000 +

2 × 1000 +

7 × 100 +

0 × 10 +

5 × 1 +

6 ÷ 10 +

8 ÷ 100 +

4 ÷ 1000.

Обратите внимание на знаки деления. Затем я представил эту последовательность операций без деления:

4 × 10 000 +

2 × 1000 +

7 × 100 +

0 × 10 +

5 × 1 +

6 × 0,1 +

8 × 0,01 +

4 × 0,001.

И наконец, отобразил это число, используя степени числа 10:

4 × 104 +

2 × 103 +

7 × 102 +

0 × 101 +

5 × 100 +

6 × 10–1 +

8 × 10–2 +

4 × 10–3.

Существуют рациональные числа, которые не так легко представить в виде десятичной дроби, например ⅓. Если вы разделите 1 на 3, то получите следующее.

0,33333333333333333333333333333333333333333333333333333…

И так до бесконечности. Подобная дробь называется периодической и записывается 0,(3). Несмотря на то что запись числа ⅓ в виде десятичной дроби выглядит неуклюже, это число по-прежнему является рациональным, поскольку это отношение двух целых чисел. Вот еще один пример: отношение 1/7 можно записать в виде десятичной дроби.

0,1428571428571428571428571428571428571428571428571428571…

Или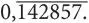

Иррациональные числа — это числа, которые нельзя выразить в виде отношения двух целых чисел, значит, десятичная дробь продолжается бесконечно без повторяющихся последовательностей цифр. К числам такого типа относится квадратный корень из 2.