Аркадий Липкин - Концепции современного естествознания. Часть 1. Науки о неживом (физика, химия, синергетика)

Но, с другой стороны, волны могут рассматриваться как системы. Причем так же как различные механические системы собираются из частиц, волны (это может быть одиночный импульс, цуг, состоящий из нескольких импульсов, и т. д.) собираются из простейших, так называемых гармонических, или синусоидальных, волн. Все прочие волны можно представить в виде суммы синусоидальных волн. При этом линейные волны подчиняются принципу суперпозиции, т. е. они распространяются независимо друг от друга. Таким образом гармонические, или синусоидальные, волны играют здесь роль ПИО, которые характеризуются частотой (подобно тому, как механические частицы характеризуются массой). Направление распространения гармонической волны, ее амплитуда, начальная фаза, поляризация характеризуют ее состояние. Они меняются под действием затухания, фильтров, поляризаторов, фазовых пластин, зеркал и т. п., выступающих в роли внешних воздействий («сил»). Волны имеют передний и задний фронты (начало и конец, расстояние между которыми определяет еще один важный параметр волны – ее «длину когерентности»).

То есть волна представляет собой протяженный, но локальный (ограниченный) объект, движущийся в пространстве. Поэтому многое в их поведении напоминает поведение частиц. Не случайно в течение долгого времени конкурировали волновая и корпускулярная модели распространения света. Тем не менее исходно они выступают как альтернативные модели. Специфическими свойствами волн, характеризующими их распространение как принципиально отличное от движения частиц, являются свойства интерференции (термин, введенный Томасом Юнгом в 1803 г.) и дифракции (явление огибания тела волной, из-за чего предсказываемые геометрической оптикой резкие тени размываются). Эти свойства отличают поведение волн от поведения потока частиц, описываемого законами геометрической оптики.

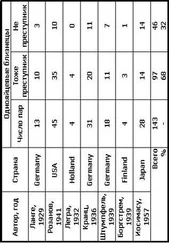
Наиболее ярким является свойство интерференции : две совпадающие по частоте и имеющие неизменную разность фаз («когерентные») волны могут находиться как «в фазе» (максимум (гребень) под максимумом – слева на рис. 5.1), так и «в противофазе» (максимум (гребень) под минимумом (впадиной)– справа на рис. 5.1). В первом случае они складываются, во втором – вычитаются.

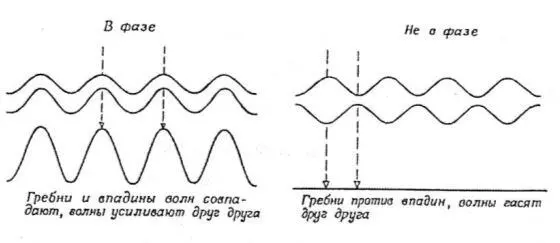
Рис. 5.1

В результате возможна ситуация, когда сложение двух волн приводит к их взаимоуничтожению (аннигиляции). Такая ситуация для классических частиц невозможна 14 14 Возможна аннигиляция квантовых частиц в релятивистской квантовой механике, но квантовые частиц, как мы увидим, обладают этими волновыми свойствами. . Поэтому данное явление – наличие светлой точки в центре тени от диска – однозначно указывает на волну. И когда Томас Юнг показал, что свет обладает этим свойством, то спор о природе света был решен в пользу волн.

Поскольку кроме рассмотренных крайних случаев возможны и все промежуточные, то общая картина интерференции может выглядеть более сложно. В общем случае при приходе двух совпадающих по частоте и имеющих неизменную разность фаз (когерентных) волн в точках среды, куда обе волны приходят в фазе, они усиливают друг друга, а в точках, куда они приходят в противофазе, – ослабляют. В результате получается картина так называемых интерференционных полос. В частности, в случае пучка света, падающего перпендикулярно на экран с двумя щелями, на стоящем за ним параллельном экране максимум интенсивности наблюдается в центре геометрической тени. На сечении экрана плоскостью, проходящей через середину между щелями перпендикулярно экранам, наблюдается максимум интенсивности света, и это будет повторяться при разности расстояний до щелей кратной длине волны. В интервале между этими максимумами интенсивность света будет убывать к середине этого интервала, где освещенность будет равна нулю, так как световые волны от двух щелей приходят туда в противофазе. Эта картина изображена на правой части рис. 7.2, где справа изображен график интенсивности суммарной волны. Это классический опыт по доказательству волнового (а не корпускулярного, как предполагал Ньютон) характера света.

Явление дифракции состоит в огибании резкой границы волной (правая часть рис. 5.2), из-за чего предсказываемые геометрической оптикой резкие тени размываются.

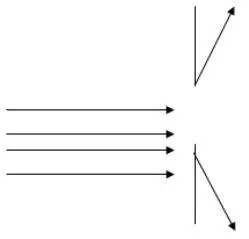
Рис. 5.2