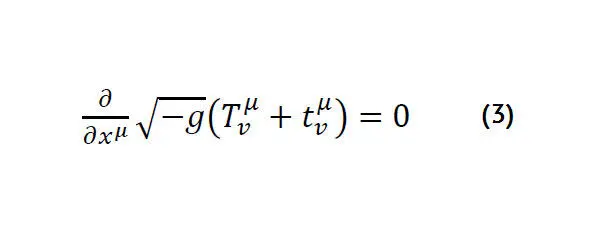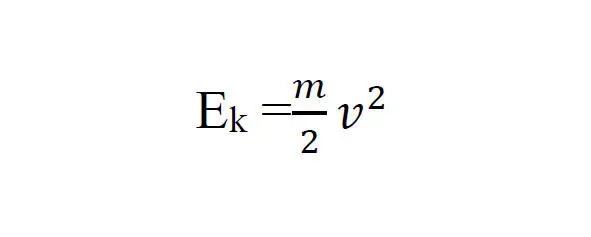Анатолий Трутнев - Новый сборник статей по физике пространства. Наука будущего

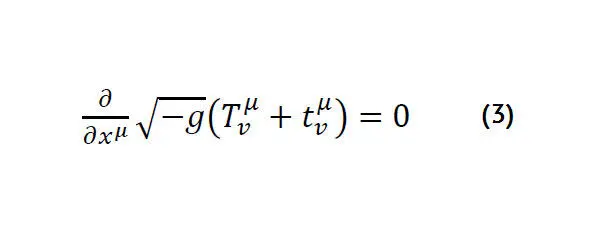
где Т μ υэнергия-импульс материи

t μ υ энергия-импульс гравитационного поля.

Но величина представляет собой псевдотензор и приписываемый ему отрицательный вклад гравитационного поля в общую энергию не состоятелен. На самом деле он положителен, а это лишает смысла саму идею. Некоторые физики определяют тензор энергии-импульса гравитационного поля как тензор Эйнштейнаи и она точно уравновешивает энергию – импульс материи в любом объеме, тогда их сумма тождественно равна нулю, но это утверждение не нашло всеобщего признания.

Таким образом, выше приведенный литературный обзор проблемы закона сохранения энергии в ОТО, о не разрешимости которой ещё в одной из последних работ в 1946 году писал Эйнштейн [5], несмотря на усилия многих ученых, остаётся неразрешимой до сих пор.

Для более глубокого осмысления взаимосвязи материи и пространства была смоделирована система, в основу которой были положены утверждения Эйнштейна:

– Если исчезнет материя, то исчезнет и пространство;

– Все в физическом мире держится на взаимном отталкивании и притяжении.

ПРИНЦИПЫ МОДЕЛИРОВАНИЯ

Изложены в статье «Образование химических элементов в недрах звезд-результа взаимодействия материи и пространства.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

В соответствии с базовыми принципами смоделированной системы энергия является формой взаимосвязи материи и пространства. В всех процессах, протекающих в физическом мире, имеет место обмен энергиями между материей и пространством. При этом энергия матери (E m) переходит в энергию пространства ( – E p) и наоборот, а их общая сумма (E s) равна нулю. В этом и заключается фундаментальность закона сохранения энергии или вернее превращение одних видов энергии в другие.

Примеры.

1. Тело с массой m движется вертикально вверх, совершая работу (А) против силы тяжести.

A = mgh

На это затрачивается сообщенная телу кинетическая энергия (E k)

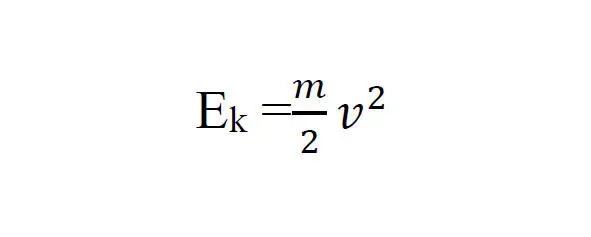
При движении тела вертикально вверх оно движется в силовых линиях пространства деформированных (сжатых) массой Земли, при этом кинетическая энергия, а это энергия материи, переходит в энергию пространства и расширяет силовые линии пространства в направлении действия сил тяжести, В результате силовые линии пространства деформируются (сжимаются) в направлении противоположном действию сил тяжести и тело движется от Земли. Как только степени деформации (сжатия) впереди и сзади тела сравниваются, а это происходит в момент полного перехода энергии материи (E k) в энергию пространства (E P), тело начинает движение по силовым линиям пространства в обратном направлении, то есть к Земле

E m+ ( – E p) = 0

При движении тела по силовым линиям пространства по направлению к Земле также происходит сжатие их в этом направлении с выделением энергии материи, затраченной массой Земли на их сжатие. В результате энергия пространства переходит в энергию материи и тело приобретает кинетическую (механическую) энергию движения к центру Земли. В следствие того, что степень деформации (сжатия) силовых линий пространства увеличивается по мере приближения к Земле, возрастает и величина выделяющейся энергии. В результате тело движется с ускорением.

В процессе фотосинтеза энергия света (E) переходит в энергию пространства (E). При этом 70% её затрачивается на образование сложных молекул органических веществ (глюкоза) из молекул простых неорганических веществ (вода, углекислый газ), а 30% её запасается в химических связях молекул органических веществ (Рис.1).

3. В процессе дыхания молекулы кислорода вступают в химические реакции с молекулами органических веществ и окисляют их. При этом внешние (валентные) электроны атомов кислорода расширяют силовые линии пространства в химических связях в сложных молекулах органических веществ, связи разрываются, атомы кислорода присоединяются к атомам, составляющим молекулу органических веществ. В результате энергия пространства переходит в энергию матери и в виде тепловой энергии.

Таким образом, исходя из утверждения одного из основных принципов смоделированной системы о том, что формой взаимосвязи материи и пространства является обмен между ними энергиями (E и —E), которые одинаковые по модулю и противоположны по знаку, формулу (3) можно переписать в следующим виде: